
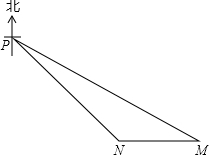
 如图,某海岛上有一观测点P,一天上午9:00观测到一轮船在点M处,M在观测点P南偏东60°方向上,渔船由东向西匀速航行跟踪鱼群,当天上午9:30渔船行至点N处,N在观测点P的东南方向上,已知该渔船的速度为每小时40海里.
如图,某海岛上有一观测点P,一天上午9:00观测到一轮船在点M处,M在观测点P南偏东60°方向上,渔船由东向西匀速航行跟踪鱼群,当天上午9:30渔船行至点N处,N在观测点P的东南方向上,已知该渔船的速度为每小时40海里.分析 (1)根据路程=速度×时间,即可求得该渔船从M到N的距离;
(2)延长MN与过点P的南北方向交于点D,则MN⊥PD于D,在Rt△PMD和Rt△PND中,根据三角函数定义MD,ND就可以PD表示出来,根据MN=20海里,就得到一个关于PD的方程,求得PD即可.
解答 解:(1)该渔船从M到N的距离为:40×$\frac{1}{2}$=20(海里); (2)如图,延长MN与过点P的南北方向交于点D,则MN⊥PD于D.
(2)如图,延长MN与过点P的南北方向交于点D,则MN⊥PD于D.
设PD为x,
在Rt△PMD中,
∵∠PDM=90°,∠DPM=60°,∠M=90°-60°=30°,
∴MD=$\sqrt{3}$PD=$\sqrt{3}$x,
在Rt△PND中,
∵∠PDN=90°,∠DPN=45°,
∴DN=PD=x.
∵MD-DN=MN,
∴$\sqrt{3}$x-x=20,
∴x=10($\sqrt{3}$+1)≈27.
答:离观测点P的最近距离约为27海里.
点评 本题主要考查解直角三角形的应用-方向角问题,构造直角三角形是解题的前提和关键.


科目:初中数学 来源: 题型:选择题
 有理数a,b在数轴上的位置如图所示,则下列判断正确的是( )
有理数a,b在数轴上的位置如图所示,则下列判断正确的是( )| A. | $\frac{a}{b}$>0 | B. | a+b>0 | C. | |a|<|b| | D. | a-b<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥弦BC于点M,若⊙O的半径为4,则OM和$\widehat{BC}$的长分别为( )
如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥弦BC于点M,若⊙O的半径为4,则OM和$\widehat{BC}$的长分别为( )| A. | 2,$\frac{π}{3}$ | B. | 2$\sqrt{3}$,π | C. | $\sqrt{3}$,$\frac{2π}{3}$ | D. | 2$\sqrt{3}$,$\frac{4π}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{{2}^{4022}}$ | B. | $\frac{1}{{2}^{4024}}$ | C. | $\frac{1}{{2}^{4026}}$ | D. | $\frac{1}{{2}^{4028}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 坐姿不良 | 站姿不良 | 走姿不良 | 三姿良好 |
| 100 | 155 | 185 | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com