练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．如图，抛物线的顶点为D点，它与y轴交于点C，与x轴交于A、B两点，A（-1，0），B（3，0），$tan∠ACO=\frac{1}{3}$．
    （1）求此抛物线的顶点坐标；
    （2）在抛物线上是否存在一点P，使∠ACP=90°，若存在，请求出点P的坐标，若不存在，请说明理由；
    （3）在抛物线的对称轴上是否存在一点Q，使|QB-QC|最大，若存在，请求出点Q的坐标，若不存在，请说明理由；
    （4）若点E在x轴上，点Q在抛物线上，若以A、C、E、Q为顶点的四边形是平行四边形，请直接写出所有符合条件的E点坐标．

    分析 （1）如图1，根据已知得出点C的坐标，利用待定系数法求二次函数的解析式；
    （2）如图2，存在，设P（x，-x2+2x+3），根据同角的余角相等得∠ACO=∠DPC，利用同角的三角函数值相等列式得$\frac{{x}^{2}-2x}{x}=\frac{1}{3}$，求出x的值，根据函数关系式求出y，写出点P的坐标；
    （3）当Q、A、C在同一直线上时，QA-QC最大为AC，即|QB-QC|最大，求直线AC与对称轴的交点坐标，就是点Q；
    （4）当A、C、E、Q为顶点的四边形是平行四边形，有四种情况：①一边与x轴平行时点E坐标为（1，0）和（-3，0）；②当点Q的纵坐标y=-3时，存在两种情况分别求出即可．

    解答 解：（1）如图1，∵A（-1，0），
    ∴OA=1，
    ∵$tan∠ACO=\frac{1}{3}$，
    ∴$\frac{OA}{OC}$=$\frac{1}{3}$，
    ∴OC=3，
    ∴C（0，3），
    设抛物线的解析式为：y=ax2+bx+c，
    把A、B、C三点的坐标分别代入得：$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$，
    解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$，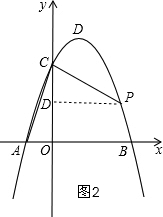
    ∴抛物线的解析式为：y=-x2+2x+3=-（x-1）2+4，
    ∴顶点坐标为（1，4）；
    （2）如图2，存在，设P（x，-x2+2x+3），则OD=-x2+2x+3，CD=3-OD=3-（-x2+2x+3）=x2-2x，
    过P作PD⊥y轴于D，
    ∵∠ACP=90°，
    ∴∠ACO+∠OCP=90°，
    ∵∠CDP=90°，
    ∴∠DPC+∠OCP=90°，
    ∴∠ACO=∠DPC，
    ∴tan∠DPC=$\frac{CD}{PD}$=$\frac{1}{3}$，
    则$\frac{{x}^{2}-2x}{x}=\frac{1}{3}$，
    解得：x1=0，x2=$\frac{7}{3}$，
    经检验：x=$\frac{7}{3}$是原方程的根，
    当x=$\frac{7}{3}$时，y=-（$\frac{7}{3}$-1）2+4=$\frac{20}{9}$，
    ∴P（$\frac{7}{3}$，$\frac{20}{9}$）；
    （3）如图3，存在，
    ∵点Q在对称轴上，
    ∴QA=QB，
    在△QAC中，QA-QC＜AC，
    ∴当Q、A、C在同一直线上时，QA-QC最大为AC，即|QB-QC|最大，
    设直线AC的解析式为：y=kx+b，
    把A（-1，0）、C（0，3）代入得：$\left\{\begin{array}{l}{-k+b=0}\\{b=3}\end{array}\right.$，
    解得$\left\{\begin{array}{l}{k=3}\\{b=3}\end{array}\right.$，
    ∴直线AC的解析式为：y=3x+3，
    当x=1时，y=6
    ∴Q（1，6）；
    （4）如图4，∵对称轴x=1，C（0，3），
    ∴CQ=2，
    ∵四边形AECQ是平行四边形，
    ∴AE=CQ=2，
    ∵A（-1，0），
    ∴E（1，0）；
    如图5，同理可得E（-3，0）；
    如图6，过Q作QG⊥x轴于G，
    ∵△AOC≌△EGQ，
    ∴EG=OA=1，OC=GQ=3，
    设Q（x，-3），
    当y=-3时，-x2+2x+3=-3，
    解得：x=1±$\sqrt{7}$，
    ∴OG=1+$\sqrt{7}$，
    ∵△AOC≌△EGQ，
    ∴EG=OA=1，
    ∴E（2+$\sqrt{7}$，0），
    如图7，设Q（x，-3），
    同理x=1-$\sqrt{7}$，
    ∴OE=$\sqrt{7}$-2，
    ∴E（2-$\sqrt{7}$，0）；
    综上所述：点E的坐标为（1，0）或（2±$\sqrt{7}$，0）或（-3，0）．

    点评 本题是二次函数的综合题，考查了利用待定系数法求二次函数的解析式；本题还与三角函数相结合，列等式求出点的坐标或边的长；第（2）问也可以利用三角形相似，对应边成比例得出；对于二次函数的最值问题，除了运用顶点坐标求以外，还可以利用三角形的三边关系求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．平面直角坐标系中，边长为 a的正方形OABC如图放置．
    （1）①如图1，直接写出点B的坐标B（a，a ）
    ②如图1，a=$\sqrt{5}$，点D为OC上一点，连接BD，分别过点C、D作BD的垂线，垂足为M、N，若CM=1，求N点的坐标；
    （2）如图2，连接对角线AC，点P为线段BC上一点（不包含B、C），以OP为直角边向上作等腰Rt△EOP，∠EOP=90°，EP交AC于H，求证：OH=$\frac{1}{2}$EP；并直接写出OH的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如果两个角的两条边分别平行，且其中一个角比另一个角3倍少20°，那么这两个角是10°、10°或130°、50°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：
    （1）（-$\frac{1}{3}$）100×3101-（π-3）0-（-2）-2    
    （2）（a+2b）（a-2b）+（a+2b）2-4ab．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：
    （1）-10-2-1×3-1×[2-（-3）2]
    （2）（x-2）（x+3）-（x-3）2
    （3）（x+y-3）（x-y+3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．如图，在平面直角坐标系中，矩形OABC的边OA，OC分别在两坐标轴的正半轴上，B点的坐标为（4，3），平行于对角线AC的一条直线m从原点O出发沿x轴正半轴方向以每秒1个单位的速度运动，直线与矩形OABC的两边分别交于点M，N，设直线的运动时间为t（秒），△OMN的面积为y，则下图哪个曲线能够最准确反映y与t之间的函数关系（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．甲、乙两地相距900km，一辆货车从甲地出发以60km∕h的速度开往乙地，另一辆轿车同时从乙地出发匀速开往甲地．图中的折线ABCD表示货车与轿车相距的距离y（km）与时间x（h）之间的函数图象，请根据图象，解答下列问题：
    （1）求轿车行驶速度；
    （2）两车出发多少小时，两车相距300km？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在?ABCD中，AC，BD相交于点O，过点O作直线EF，GH分别交平行四边形的四条边于E、G、F、H四点，连结EG、GH、FH、HE
    （1）如图①，试判断四边形EGFH的形状，并说明理由；
    （2）如图②，当EF⊥GH时，四边形EGFH的形状是菱形；
    （3）如图③，在（2）的条件下，若AC=BD，四边形EGFH的形状是菱形；
    （4）如图④，在（3）的条件下，若AC⊥BD，试判断四边形EGFH的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．8的立方根是（　　）
    A．2B．±2C．$2\sqrt{2}$D．$±2\sqrt{2}$

    查看答案和解析>>

    同步练习册答案