
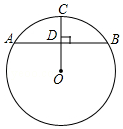
 如图,在⊙O中,弦AB垂直平分半径OC,垂足为D,若⊙O的半径为4,则弦AB的长为4$\sqrt{3}$.
如图,在⊙O中,弦AB垂直平分半径OC,垂足为D,若⊙O的半径为4,则弦AB的长为4$\sqrt{3}$.  云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 无理数是无限不循环小数 | |
| B. | 单项式-$\frac{a{b}^{2}}{3}$的系数是-$\frac{1}{3}$ | |
| C. | 近似数7.30所表示的准确数a的范围是:7.295≤a<7.305 | |
| D. | 有理数可分为整数和小数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com