
【题目】日前,某公司决定对塘栖枇杷品种进行培育,育苗基地对其中的四个品种“白砂”“红袍”“夹脚”“宝珠”共500粒种子进行发芽试验,从中选择发芽率最高的品种进行推广,通过实验得知“白砂”品种的发芽率为![]() ,并把实验数据绘成两幅统计图(部分信息未给出):
,并把实验数据绘成两幅统计图(部分信息未给出):
![]()
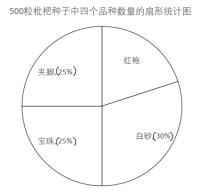
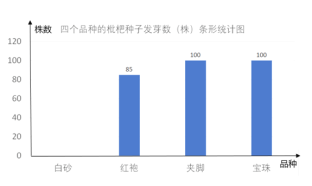
(1)求实验中“红袍”品种的种子数量;
(2)求实验中“白砂”品种的种子发芽的株数,并补全条形统计图;
(3)从以上信息,你认为应选哪一个品种进行推广,请说明理由.
【答案】(1)100;(2)图见解析;(3)应该选择“红袍”品种进行推广.
【解析】
(1)根据扇形图可知“红袍”品种的种子所占百分比,再用总数ד红袍”品种的种子所占百分比,求出“红袍”品种的种子数量.
(2)可用总数乘“白砂”品种的种子所占百分比,求出“白砂”品种的种子数量,从而补全统计图.
(3)根据条形统计图判断每个品种的种子发芽率,进而判断出推广的品种.
解:(1)“红袍”品种的种子数量:![]() (粒)
(粒)
(2)“白砂”品种的种子发芽的株数:![]() (株);
(株);
补全条形统计图如下:
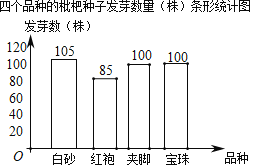 .
.
(3)“红袍”品种的种子发芽率:![]() ;
;
“宝珠”品种的种子发芽率:![]() ;
;
“夹脚”品种的种子发芽率:![]() ;
;
因此,应该选择“红袍”品种进行推广.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】据新浪网调查,在第十二届全国人大二中全会后,全国网民对政府工作报告关注度非常高,大家关注的网民们关注的热点话题分别有:消费、教育、环保、反腐、及其它共五类,且关注五类热点问题的网民的人数所占百分比如图l所示,关注该五类热点问题网民的人数的不完整条形统计如图2所示,请根据图中信息解答下列问题.
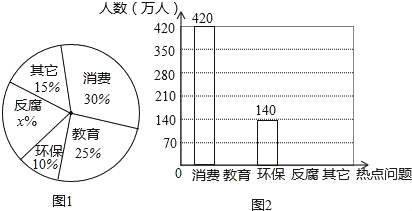
(1)求出图l中关注“反腐”类问题的网民所占百分比x的值,并将图2中的不完整的条形统计图补充完整;
(2)为了深入探讨政府工作报告,新浪网邀请成都市5名网民代表甲、乙、丙、丁、戊做客新浪访谈,且一次访谈只选2名代表,请你用列表法或画树状图的方法,求出一次所选代表恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 5 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
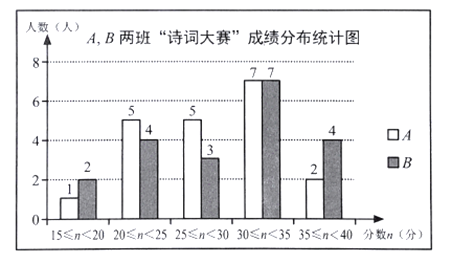
【题目】为让学生感受中华诗词之美,某校九年级举行了“诗词大赛”,为了解九年级![]() 两班学生的“诗词大赛”成绩,分别从每班
两班学生的“诗词大赛”成绩,分别从每班![]() 名学生中各随机抽取
名学生中各随机抽取![]() 人的“诗词大赛”成绩(满分为
人的“诗词大赛”成绩(满分为![]() 分,成绩均为整数),制成如图所示的统计图.
分,成绩均为整数),制成如图所示的统计图.
![]() 若将不低于
若将不低于![]() 分的成绩评为优秀,请你估计一下哪个班级优秀人数多? 多几人?
分的成绩评为优秀,请你估计一下哪个班级优秀人数多? 多几人?
![]() 请你选择适当的统计量来说明
请你选择适当的统计量来说明![]() 两班哪个班级的整体成绩较好?
两班哪个班级的整体成绩较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
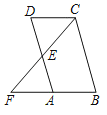
【题目】如图,四边形ABCD是平行四边形,点F在BA的延长线上,连接CF交AD于点E.
(1)求证:△CDE∽△FAE;
(2)当E是AD的中点且BC=2CD时,直接写出图中所有与∠F相等的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究发现,二次函数![]() (
(![]() )图象上任何一点到定点(0,
)图象上任何一点到定点(0,![]() )和到定直线
)和到定直线![]() 的距离相等.我们把定点(0,
的距离相等.我们把定点(0,![]() )叫做抛物线
)叫做抛物线![]() 的焦点,定直线
的焦点,定直线![]() 叫做抛物线
叫做抛物线![]() 的准线.
的准线.
(1)写出函数![]() 图象的焦点坐标和准线方程;
图象的焦点坐标和准线方程;
(2)等边三角形OAB的三个顶点都在二次函数![]() 图象上,O为坐标原点,求等边三角形的边长;
图象上,O为坐标原点,求等边三角形的边长;
(3)M为抛物线![]() 上的一个动点,F为抛物线
上的一个动点,F为抛物线![]() 的焦点,P(1,3)为定点,求MP+MF的最小值.
的焦点,P(1,3)为定点,求MP+MF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表显示的是某种大豆在相同条件下的发芽试验结果:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆的粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ①②③ B. ①② C. ①③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
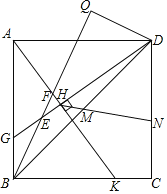
【题目】如图,Q为正方形ABCD外一点,连接BQ,过点D作DQ⊥BQ,垂足为Q,G、K分别为AB、BC上的点,连接AK、DG,分别交BQ于F、E,AK⊥DG,垂足为点H,AF=5,DH=8,F为BQ中点,M为对角线BD的中点,连接HM并延长交正方形于点N,则HN的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com