
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćA(1£¬4)£¬µćB(3£¬2)£¬Į¬½ÓOA£¬OB£®
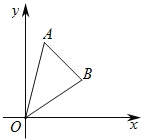
£Ø1£©ĒóÖ±ĻßOBÓėABµÄ½āĪöŹ½£»
£Ø2£©Ēó”÷AOBµÄĆ껿£®
£Ø3£©ĻĀĆęĮ½µĄŠ”Ģā£¬ČĪŃ”Ņ»µĄ×÷“š£®×÷“šŹ±£¬Ēė×¢Ć÷ĢāŗÅ£¬Čō¶ą×ö£¬Ōņ°“Ź××öĢā¼ĘČė×Ü·Ö£®
¢ŁŌŚyÖįÉĻŹĒ·ń“ęŌŚŅ»µćP£¬Ź¹”÷PABÖܳ¤×īŠ”£®Čō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćP×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
¢ŚŌŚĘ½ĆęÄŚŹĒ·ń“ęŌŚŅ»µćC£¬Ź¹ŅŌA£¬O£¬C£¬BĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£®Čō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćC×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©Ö±ĻßOBµÄ½āĪöŹ½ĪŖ![]() £¬Ö±ĻßABµÄ½āĪöŹ½ĪŖy= -x+5£Ø2£©5£»£Ø3£©¢Ł“ęŌŚ£¬(0£¬
£¬Ö±ĻßABµÄ½āĪöŹ½ĪŖy= -x+5£Ø2£©5£»£Ø3£©¢Ł“ęŌŚ£¬(0£¬![]() )£»¢Ś“ęŌŚ£¬(2£¬-2)»ņ(4£¬6)»ņ(-2£¬2)
)£»¢Ś“ęŌŚ£¬(2£¬-2)»ņ(4£¬6)»ņ(-2£¬2)
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅā·Ö±šÉč³öĮ½Ö±ĻߵĽāĪöŹ½£¬“śČėÖ±ĻßÉĻĮ½µć×ų±ź¼“æÉĒó³öÖ±ĻßOBÓėABµÄ½āĪöŹ½£»
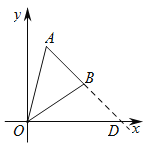
£Ø2£©ŃÓ³¤Ļ߶ĪAB½»xÖįÓŚµćD£¬Ēó³öDµÄ×ų±ź£¬·Ö±šĒó³ö![]() ”¢
”¢![]() ÓÉ
ÓÉ![]() ¼“æÉĒóµĆ£»
¼“æÉĒóµĆ£»
£Ø3£©¢Łøł¾ŻĮ½µćÖ®¼äĻ߶Ī×ī¶Ģ£¬A”¢BŌŚyÖįĶ¬²ą£¬×÷³öµćA¹ŲÓŚyµÄ¶Ō³Ęµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() BÓėyÖįµÄ½»µć¼“ĪŖĖłĒóµćP£»
BÓėyÖįµÄ½»µć¼“ĪŖĖłĒóµćP£»
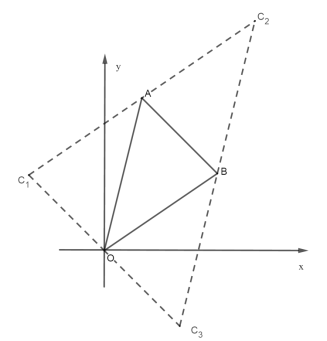
¢ŚŹ¹ŅŌA£¬O£¬C£¬BĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬Ōņ·ÖČżÖÖĒéæö·ÖĪö£¬·Ö±šŅŌOA”¢AB”¢OBĪŖ¶Ō½ĒĻß×÷³öĘ½ŠŠĖıߊĪ£¬ĄūÓĆÖŠµć×ų±ź¹«Ź½“śČėĒó½ā¼“æÉ£®
½ā£ŗ£Ø1£©ÉčÖ±ĻßOBµÄ½āĪöŹ½ĪŖy=mx£¬
”ßµćB(3£¬2)£¬
”ą![]() £¬
£¬
”ąÖ±ĻßOBµÄ½āĪöŹ½ĪŖ![]() £¬
£¬
ÉčÖ±ĻßABµÄ½āĪöŹ½ĪŖy=kx+b£¬
øł¾ŻĢāŅāæÉµĆ£ŗ![]()
½āÖ®µĆ![]()
”ąÖ±ĻßABµÄ½āĪöŹ½ĪŖy= -x+5£®
¹Ź“š°øĪŖ£ŗÖ±ĻßOBµÄ½āĪöŹ½ĪŖ![]() £¬Ö±ĻßABµÄ½āĪöŹ½ĪŖy= -x+5£»
£¬Ö±ĻßABµÄ½āĪöŹ½ĪŖy= -x+5£»
£Ø2£©ČēĶ¼£¬ŃÓ³¤Ļ߶ĪAB½»xÖįÓŚµćD£¬
µ±y=0Ź±£¬-x+5=0£¬x=5£¬
”ąµćDŗį×ų±źĪŖ5£¬OD=5£¬
”ą![]() £¬
£¬
![]()
”ą![]() £¬
£¬
¹Ź“š°øĪŖ£ŗ5£®
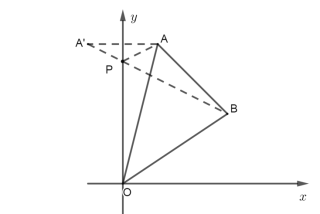
£Ø3£©¢Ł“ęŌŚ£¬(0£¬![]() )£»
)£»
¹żµćA×÷yÖįµÄ¶Ō³Ęµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() B£¬½»yÖįÓėµćP£¬ŌņµćP¼“ĪŖŹ¹”÷PABÖܳ¤×īŠ”µÄµć£¬
B£¬½»yÖįÓėµćP£¬ŌņµćP¼“ĪŖŹ¹”÷PABÖܳ¤×īŠ”µÄµć£¬
ÓÉ×÷Ķ¼æÉÖŖ£¬µć![]() ×ų±źĪŖ
×ų±źĪŖ![]() £¬ÓÖµćB£Ø3£¬2£©
£¬ÓÖµćB£Ø3£¬2£©
ŌņÖ±Ļß![]() BµÄ½āĪöŹ½ĪŖ£ŗ
BµÄ½āĪöŹ½ĪŖ£ŗ![]() £¬
£¬
”ąµćP×ų±źĪŖ![]() £¬
£¬
¹Ź“š°øĪŖ£ŗ![]() £»
£»
¢Ś“ęŌŚ£® ![]() »ņ
»ņ![]() »ņ
»ņ![]() £®
£®
ÓŠČżÖÖĒéæö£¬ČēĶ¼ĖłŹ¾£ŗÉčµćC×ų±źĪŖ![]() £¬
£¬
µ±Ę½ŠŠĖıߊĪŅŌAOĪŖ¶Ō½ĒĻߏ±£¬
ÓÉÖŠµć×ų±ź¹«Ź½æÉÖŖ£¬AOµÄÖŠµć×ų±źŗĶBCÖŠµć×ų±źĻąĶ¬£¬
”ą![]()
½āµĆ![]()
”ąµć![]() ×ų±źĪŖ
×ų±źĪŖ![]() £¬
£¬
µ±Ę½ŠŠĖıߊĪŅŌABĪŖ¶Ō½ĒĻߏ±£¬ABµÄÖŠµć×ų±źŗĶOCµÄÖŠµć×ų±źĻąĶ¬£¬Ōņ
![]()
![]()
”ąµć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £¬
£¬
µ±Ę½ŠŠĖıߊĪŅŌBOĪŖ¶Ō½ĒĻߏ±£¬BOµÄÖŠµć×ų±źŗĶACµÄÖŠµć×ų±źĻąĶ¬£¬Ōņ
![]()
½āµĆ![]()
”ąµć![]() ×ų±źĪŖ
×ų±źĪŖ![]() £¬
£¬
¹Ź“š°øĪŖ£ŗ“ęŌŚ£¬![]() »ņ
»ņ![]() »ņ
»ņ![]() £®
£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĻŲ½ĢÓż¾ÖĪŖĮĖĮĖ½āѧɜ¶ŌĢåÓżĮ¢¶ØĢųŌ¶£Ø![]() £©”¢ĢųÉž£Ø
£©”¢ĢųÉž£Ø![]() £©”¢ÖĄŹµŠÄĒņ£Ø
£©”¢ÖĄŹµŠÄĒņ£Ø![]() £©”¢ÖŠ³¤ÅÜ£Ø
£©”¢ÖŠ³¤ÅÜ£Ø![]() £©ĖÄøöĻīÄæµÄĻ²°®³Ģ¶Č£ØĆæČĖֻєŅ»Ļī£©£¬Č·¶ØÖŠæ¼ĢåÓżæ¼ŹŌĻīÄ棬ĢŲ¶Ō°ĖÄź¼¶Ä³°ą½ųŠŠĮĖµ÷²é£¬²¢»ęÖĘ³ÉČēĻĀʵŹż”¢ĘµĀŹĶ³¼Ę±ķŗĶÉČŠĪĶ³¼ĘĶ¼£ŗ
£©ĖÄøöĻīÄæµÄĻ²°®³Ģ¶Č£ØĆæČĖֻєŅ»Ļī£©£¬Č·¶ØÖŠæ¼ĢåÓżæ¼ŹŌĻīÄ棬ĢŲ¶Ō°ĖÄź¼¶Ä³°ą½ųŠŠĮĖµ÷²é£¬²¢»ęÖĘ³ÉČēĻĀʵŹż”¢ĘµĀŹĶ³¼Ę±ķŗĶÉČŠĪĶ³¼ĘĶ¼£ŗ
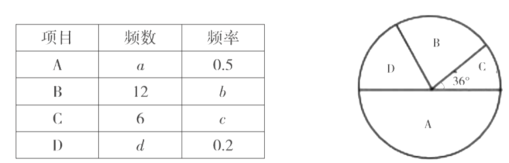
£Ø1£©Ēó³öÕā“Īµ÷²éµÄ×ÜČĖŹż£»
£Ø2£©Ēó³ö±ķÖŠ![]() µÄÖµ£»
掙术
£Ø3£©ČōøĆŠ£°ĖÄź¼¶ÓŠŃ§Éś1200ČĖ£¬ĒėÄćĖć³öĻ²°®ĢųÉžµÄČĖŹż£¬²¢·¢±ķÄćµÄæ“·Ø£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB£½AC£¬ADŹĒBC±ßÉĻµÄøߣ¬µćE”¢FŹĒADµÄČżµČ·Öµć£¬ČōAD£½6cm£¬CD£½3cm£¬ŌņĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿ŹĒ____cm2£®
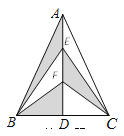
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æA”¢BĮ½Į¾Ęū³µĶ¬Ź±“ÓĻą¾ą330Ē§Ć׵ļה¢ŅŅĮ½µŲĻąĻņ¶ųŠŠ£¬s£ØĒ§Ć×£©±ķŹ¾Ęū³µÓė¼×µŲµÄ¾ąĄė£¬t£Ø·Ö£©±ķŹ¾Ęū³µŠŠŹ»µÄŹ±¼ä£¬ČēĶ¼£¬L1£¬L2·Ö±š±ķŹ¾Į½Į¾Ęū³µµÄsÓėtµÄ¹ŲĻµ£®
£Ø1£©L1±ķŹ¾ÄÄĮ¾Ęū³µµ½¼×µŲµÄ¾ąĄėÓėŠŠŹ»Ź±¼äµÄ¹ŲĻµ£æ
£Ø2£©Ęū³µBµÄĖŁ¶ČŹĒ¶ąÉŁ£æ
£Ø3£©ĒóL1£¬L2·Ö±š±ķŹ¾µÄĮ½Į¾Ęū³µµÄsÓėtµÄ¹ŲĻµŹ½£®
£Ø4£©2Š”Ź±ŗó£¬Į½³µĻą¾ą¶ąÉŁĒ§Ć×£æ
£Ø5£©ŠŠŹ»¶ą³¤Ź±¼äŗó£¬A”¢BĮ½³µĻąÓö£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy1=a£Øx+2£©2©3Óėy2=![]() £Øx©3£©2+1½»ÓŚµćA£Ø1£¬3£©£¬¹żµćA×÷xÖįµÄĘ½ŠŠĻߣ¬·Ö±š½»Į½ĢõÅ×ĪļĻßÓŚµćB£¬C£®ŌņŅŌĻĀ½įĀŪ£ŗ
£Øx©3£©2+1½»ÓŚµćA£Ø1£¬3£©£¬¹żµćA×÷xÖįµÄĘ½ŠŠĻߣ¬·Ö±š½»Į½ĢõÅ×ĪļĻßÓŚµćB£¬C£®ŌņŅŌĻĀ½įĀŪ£ŗ
¢ŁĪŽĀŪxČ”ŗĪÖµ£¬y2µÄÖµ×ÜŹĒÕżŹż£»
¢Śa=1£»
¢Ūµ±x=0Ź±£¬y2©y1=4£»
¢Ü2AB=3AC£»
ĘäÖŠÕżČ·½įĀŪŹĒ£Ø””””£©
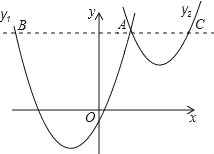
A. ¢Ł¢Ś B. ¢Ś¢Ū C. ¢Ū¢Ü D. ¢Ł¢Ü
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬E”¢F”¢G”¢H·Ö±šŹĒĖıߊĪABCD±ßAB”¢BC”¢CD”¢ADµÄÖŠµć£¬ĻĀĮŠĖµ·ØÕżČ·µÄŹĒ£Ø””””£©
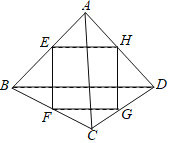
A.µ±AC”ĶBDŹ±£¬ĖıߊĪEFGHŹĒĮāŠĪ
B.µ±AC£½BDŹ±£¬ĖıߊĪEFGHŹĒ¾ŲŠĪ
C.µ±ĖıߊĪABCDŹĒĘ½ŠŠĖıߊĪŹ±£¬ŌņĖıߊĪEFGHŹĒ¾ŲŠĪ
D.µ±ĖıߊĪABCDŹĒ¾ŲŠĪŹ±£¬ŌņĖıߊĪEFGHŹĒĮāŠĪ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µõ³µŌŚĖ®Ę½µŲĆęÉĻµõĘš»õĪļŹ±£¬µõÉžBCÓėµŲĆę±£³Ö“¹Ö±£¬µõ±ŪABÓėĖ®Ę½ĻߵļŠ½ĒĪŖ64”ć£¬µõ±Ūµ×²æA¾ąµŲĆę1.5m£®£Ø¼ĘĖć½į¹ū¾«Č·µ½0.1m£¬²Īæ¼Źż¾Żsin64”ć”Ö0.90£¬cos64”ć”Ö0.44£¬tan64”ć”Ö2.05£©
£Ø1£©µ±µõ±Ūµ×²æAÓė»õĪļµÄĖ®Ę½¾ąĄėACĪŖ5mŹ±£¬µõ±ŪABµÄ³¤ĪŖ”” ””m£®
£Ø2£©Čē¹ūøƵõ³µµõ±ŪµÄ×ī“󳤶ČADĪŖ20m£¬ÄĒĆ““ÓµŲĆęÉĻµõĘš»õĪļµÄ×ī“óø߶ȏĒ¶ąÉŁ£æ£Øµõ¹³µÄ³¤¶ČÓė»õĪļµÄø߶ČŗöĀŌ²»¼Ę£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
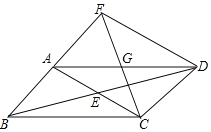
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬Ę½ŠŠĖıߊĪABCD£¬¶Ō½ĒĻßACÓėBDĻą½»ÓŚµćE£¬µćGĪŖADµÄÖŠµć£¬ĒŅAG£½AB”¢CGµÄŃÓ³¤Ļß½»BAµÄŃÓ³¤ĻßÓŚµćF£¬Į¬½ÓFD£®ŹŌĢ½¾æµ±”ĻBCD£½”” ”揱£¬ĖıߊĪACDFŹĒ¾ŲŠĪ£¬Ö¤Ć÷ÄćµÄ½įĀŪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¹ŲÓŚ![]() µÄ·½³Ģ
µÄ·½³Ģ![]() ÓŠĮ½øö²»ĻąµČµÄŹµŹżøł
ÓŠĮ½øö²»ĻąµČµÄŹµŹżøł![]() ”¢
”¢![]() £®
£®
£Ø1£©Ēó![]() µÄȔֵ·¶Ī§£»
µÄȔֵ·¶Ī§£»
£Ø2£©ŹĒ·ń“ęŌŚŹµŹż![]() £¬Ź¹·½³ĢĮ½ŹµŹżøł»„ĪŖĻą·“Źż£æČē¹ū“ęŌŚ£¬Ēó³ö
£¬Ź¹·½³ĢĮ½ŹµŹżøł»„ĪŖĻą·“Źż£æČē¹ū“ęŌŚ£¬Ēó³ö![]() µÄÖµ£¬Čē²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
µÄÖµ£¬Čē²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com