
ĄŸÌâÄżĄżÒŃÖȘÔÚÆœĂæÖ±œÇŚű±êÏ”xOyÖĐŁŹĆŚÎïÏßy1=ax2+bxŁšaĄÙ0Ł©ŁŹÓëxÖáŐę°ëÖ᜻ÓÚ”ăA1Łš2ŁŹ0Ł©ŁŹ¶„”ăÎȘP1 ŁŹ ĄśOP1A1ÎȘŐęÈęœÇĐÎŁŹÏÖœ«ĆŚÎïÏßy1=ax2+bxŁšaĄÙ0Ł©ŃŰÉäÏßOP1ÆœÒÆŁŹ°Ńčę”ăA1ʱ”ÄĆŚÎïÏߌÇÎȘĆŚÎïÏßy2 ŁŹ ŒÇĆŚÎïÏßy2ÓëxÖá”ÄÁíÒ»œ»”ăÎȘA2Ł»°ŃĆŚÎïÏßy2ŒÌĐűŃŰÉäÏßOP1ÆœÒÆŁŹ°Ńčę”ăA2ʱ”ÄĆŚÎïÏߌÇÎȘĆŚÎïÏßy3 ŁŹ ŒÇĆŚÎïÏßy3ÓëxÖá”ÄÁíÒ»œ»”ăÎȘA3Ł»ĄŁźŁ»°ŃĆŚÎïÏßy2015ŒÌĐűŃŰÉäÏßOP1ÆœÒÆŁŹ°Ńčę”ăA2015ʱ”ÄĆŚÎïÏߌÇÎȘĆŚÎïÏßy2016 ŁŹ ŒÇĆŚÎïÏßy2016ÓëxÖá”ÄÁíÒ»œ»”ăÎȘA2016 ŁŹ ¶„”ăÎȘP2016 Łź ÈôŐâ2016ÌőĆŚÎïÏߔĶ„”ă¶ŒÔÚÉäÏßOP1ÉÏŁź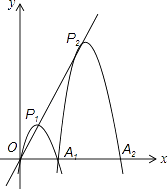
Łš1Ł©ąÙÇóĄśOP1A1”ÄĂæ»ęŁ»ąÚÇóaŁŹb”ÄÖ”Ł»
Łš2Ł©ÇóĆŚÎïÏßy2”ÄœâÎöÊœŁ»
Łš3Ł©ÇëÖ±œÓĐŽłö”ăA2016ÒÔŒ°”ăP2016Śű±êŁź
ĄŸŽđ°žĄż
Łš1Ł©
œâŁșąÙčę”ăP1ŚśŚśP1B1ĄÍxÖᣏŽčŚăÎȘB1Łź

ĄßĄśOP1A1ÎȘŐęÈęœÇĐÎŁŹ
ĄàĄÏP1OA1=60ĄăŁŹP1O=P1A1Łź
ÓÖĄßP1B1ĄÍxÖᣏ
Ąà0B1=B1A1=1Łź
ĄàP1B1=OP1ĄÁ ![]() =2ĄÁ
=2ĄÁ ![]() =
= ![]() Łź
Łź
ĄàP1Łš1ŁŹ ![]() Ł©ŁŹĄśOP1A1”ÄĂæ»ę=
Ł©ŁŹĄśOP1A1”ÄĂæ»ę= ![]() OA1P1B1=
OA1P1B1= ![]() ĄÁ2ĄÁ
ĄÁ2ĄÁ ![]() =
= ![]() Łź
Łź
ąÚĄßœ«”ăA1Łš2ŁŹ0Ł©ĄąP1Łš1ŁŹ ![]() Ł©ÔÚĆŚÎïÏßy1ÉÏŁŹ
Ł©ÔÚĆŚÎïÏßy1ÉÏŁŹ
Ąà ![]() ŁŹœâ”ĂŁșa=©
ŁŹœâ”ĂŁșa=© ![]() ŁŹb=2
ŁŹb=2 ![]()
Łš2Ł©
œâŁșÉèÖ±ÏßOP1”ÄœâÎöÊœÎȘy=kxŁź
Ąßœ«P1Łš1ŁŹ ![]() Ł©ŽúÈë”ĂŁșk=
Ł©ŽúÈë”ĂŁșk= ![]() ŁŹ
ŁŹ
ĄàÖ±ÏßOP1”ÄœâÎöÊœÎȘy= ![]() xŁź
xŁź
Ąß”ăP2ÔÚÖ±ÏßOP1ÉÏŁŹ
ĄàÉè”ăP2ŁšaŁŹ ![]() Ł©Łź
Ł©Łź
Ąày2=© ![]() Łšx©aŁ©2+
Łšx©aŁ©2+ ![]() aŁź
aŁź
Ąßœ«”ăA1”ÄŚű±êŽúÈë”ĂŁș© ![]() Łš2©aŁ©2+
Łš2©aŁ©2+ ![]() a=0ŁŹœâ”ĂŁșa1=1ŁšÉáÈ„Ł©ŁŹa2=4ŁŹ
a=0ŁŹœâ”ĂŁșa1=1ŁšÉáÈ„Ł©ŁŹa2=4ŁŹ
Ąày2=© Łšx©4Ł©2+4
![]() ŁŹŐûÀí”ĂŁșy2=©
ŁŹŐûÀí”ĂŁșy2=© ![]() x2+8
x2+8 ![]() x©12
x©12 ![]()
Łš3Ł©
œâŁșĄßa2=4ŁŹ
ĄàP2Łš4ŁŹ4 ![]() Ł©Łź
Ł©Łź
Ąà”ăA1ÓëD”ăA2čŰÓÚx=4¶ÔłÆŁŹ
Ąà”ăA2Łš6ŁŹ0Ł©Łź
ÉèP3ŁšbŁŹ ![]() Ł©Ôòy3=©
Ł©Ôòy3=© ![]() Łšx©bŁ©2+
Łšx©bŁ©2+ ![]() bŁź
bŁź
Ąßœ«A2Łš6ŁŹ0Ł©ŽúÈë”Ă© ![]() Łš6©bŁ©2+
Łš6©bŁ©2+ ![]() b=0ŁŹœâ”ĂŁșb1=4ŁšÉáÈ„Ł©ŁŹb2=9ŁŹ
b=0ŁŹœâ”ĂŁșb1=4ŁšÉáÈ„Ł©ŁŹb2=9ŁŹ
ĄàP3Łš9ŁŹ9 ![]() Ł©Łź
Ł©Łź
ĄßA2Łš6ŁŹ0Ł©ŁŹ”ăA2ÓëA3čŰÓÚx=9¶ÔłÆŁŹ
ĄàA3Łš12ŁŹ0Ł©Łź
P1Łš1ŁŹ ![]() Ł©ŁŹA1Łš2ŁŹ0Ł©ŁŹ
Ł©ŁŹA1Łš2ŁŹ0Ł©ŁŹ
P2Łš4ŁŹ4 ![]() Ł©ŁŹA2Łš6ŁŹ0Ł©ŁŹ4=22ŁŹ6=2ĄÁ3Ł»
Ł©ŁŹA2Łš6ŁŹ0Ł©ŁŹ4=22ŁŹ6=2ĄÁ3Ł»
P3Łš9ŁŹ9 ![]() Ł©ŁŹA3Łš12ŁŹ0Ł©ŁŹ9=32ŁŹ12=3ĄÁ4Ł»
Ł©ŁŹA3Łš12ŁŹ0Ł©ŁŹ9=32ŁŹ12=3ĄÁ4Ł»
Ą
P2016Łš4064256ŁŹ4064256 ![]() Ł©ŁŹA2016Łš4066272ŁŹ0Ł©
Ł©ŁŹA2016Łš4066272ŁŹ0Ł©
ĄŸœâÎöĄżŁš1Ł©ąÙčę”ăP1ŚśŚśP1B1ĄÍxÖᣏŽčŚăÎȘB1 Łź ÓɔȱßÈęœÇĐΔÄĐÔÖÊżÉÖȘżÉÇó”ĂP1B1”Äł€¶ÈŁŹÈ»șóÒÀŸĘÈęœÇĐΔÄĂæ»ęč«ÊœżÉÇó”ĂĄśOP1A1”ÄĂæ»ęŁ»ąÚœ«”ăA1Łš2ŁŹ0Ł©ĄąP1Łš1ŁŹ ![]() Ł©ŽúÈëĆŚÎïÏߔĜâÎöÊœŁŹŒŽżÉÇó”ĂaĄąb”ÄÖ”Ł»Łš2Ł©ÏÈÀûÓĂŽę¶šÏ”Êę·šÇó”ĂÖ±ÏßOP1”ÄœâÎöÊœŁŹÈ»șóÉè”ăP2ŁšaŁŹ
Ł©ŽúÈëĆŚÎïÏߔĜâÎöÊœŁŹŒŽżÉÇó”ĂaĄąb”ÄÖ”Ł»Łš2Ł©ÏÈÀûÓĂŽę¶šÏ”Êę·šÇó”ĂÖ±ÏßOP1”ÄœâÎöÊœŁŹÈ»șóÉè”ăP2ŁšaŁŹ ![]() Ł©ŁźÔòy2=©
Ł©ŁźÔòy2=© ![]() Łšx©aŁ©2+
Łšx©aŁ©2+ ![]() aŁŹœÓÏÂÀŽŁŹœ«”ăA1”ÄŚű±êŽúÈëżÉÇó”Ăa”ÄÖ”ŁŹŽÓ¶űżÉ”Ă”œĆŚÎïÏߔĜâÎöÊœŁ»Łš3Ł©ÓÉa2=4ŁŹżÉÇó”Ă”ăP2Łš4ŁŹ4
aŁŹœÓÏÂÀŽŁŹœ«”ăA1”ÄŚű±êŽúÈëżÉÇó”Ăa”ÄÖ”ŁŹŽÓ¶űżÉ”Ă”œĆŚÎïÏߔĜâÎöÊœŁ»Łš3Ł©ÓÉa2=4ŁŹżÉÇó”Ă”ăP2Łš4ŁŹ4 ![]() Ł©ŁŹÈ»șóÒÀŸĘĆŚÎïÏߔĶԳÆĐÔżÉÇó”Ă”ăA2Łš6ŁŹ0Ł©ŁŹœÓÏÂÀŽŁŹÔÙÇó”ĂP3Łš9ŁŹ9
Ł©ŁŹÈ»șóÒÀŸĘĆŚÎïÏߔĶԳÆĐÔżÉÇó”Ă”ăA2Łš6ŁŹ0Ł©ŁŹœÓÏÂÀŽŁŹÔÙÇó”ĂP3Łš9ŁŹ9 ![]() Ł©ŁŹA3Łš12ŁŹ0Ł©ŁŹŚîșóčÛČìËù”ĂœáčûŐÒłöÆäÖĐ”ÄčæÂÉŁŹÒÀŸĘčæÂÉżÉÇó”ĂÎÊÌâ”Ď𰞣ź
Ł©ŁŹA3Łš12ŁŹ0Ł©ŁŹŚîșóčÛČìËù”ĂœáčûŐÒłöÆäÖĐ”ÄčæÂÉŁŹÒÀŸĘčæÂÉżÉÇó”ĂÎÊÌâ”Ď𰞣ź
ĄŸżŒ”ăŸ«ÎöĄżÍščęÁé»îÔËÓĂÊęÓëÊœ”ÄčæÂÉŁŹŐÆÎŐÏÈŽÓÍŒĐÎÉÏŃ°ŐÒčæÂÉŁŹÈ»șóŃéÖ€čæÂÉŁŹÓŠÓĂčæÂÉŁŹŒŽÊęĐÎœáșÏŃ°ŐÒčæÂÉŒŽżÉÒÔœâŽđŽËÌ⣟


 ĂûĐŁżÎÌĂÏ”ÁĐŽđ°ž
ĂûĐŁżÎÌĂÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŁš1Ł©ÔĶÁÀíœâŁș
ÈçÍŒąÙŁŹÔÚĄśABCÖĐŁŹÈôAB=10ŁŹAC=6ŁŹÇóBC±ßÉÏ”ÄÖĐÏßAD”ÄÈĄÖ”·¶Î§Łź
œâŸöŽËÎÊÌâżÉÒÔÓĂÈçÏ·œ·šŁșŃÓł€AD”œ”ăEÊčDE=ADŁŹÔÙÁŹœÓBEŁš»òœ«ĄśACDÈÆŚĆ”ăDÄæʱŐëĐęŚȘ180Ąă”Ă”œĄśEBDŁ©ŁŹ°ŃABĄąACŁŹ2ADŒŻÖĐÔÚĄśABEÖĐŁŹÀûÓĂÈęœÇĐÎÈę±ß”ÄčŰÏ”ŒŽżÉĆĐ¶ÏŁź
ÖĐÏßAD”ÄÈĄÖ”·¶Î§ÊÇ Ł»
Łš2Ł©ÎÊÌâœâŸöŁș
ÈçÍŒąÚŁŹÔÚĄśABCÖĐŁŹDÊÇBC±ßÉÏ”ÄÖД㣏DEĄÍDFÓÚ”ăDŁŹDEœ»ABÓÚ”ăEŁŹDFœ»ACÓÚ”ăFŁŹÁŹœÓEFŁŹÇóÖ€ŁșBE+CFŁŸEFŁ»
Łš3Ł©ÎÊÌâÍŰŐčŁș
ÈçÍŒąÛŁŹÔÚËıßĐÎABCDÖĐŁŹĄÏB+ĄÏD=180ĄăŁŹCB=CDŁŹĄÏBCD=140ĄăŁŹÒÔÎȘ¶„”ăŚśÒ»žö70ĄăœÇŁŹœÇ”ÄÁœ±ß·Ö±đœ»ABŁŹADÓÚEĄąFÁœ”㣏ÁŹœÓEFŁŹÌœËśÏ߶ÎBEŁŹDFŁŹEFÖźŒä”ÄÊęÁżčŰÏ”ŁŹČąŒÓÒÔրÜŁź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹĄŃOÊÇ”È±ßĄśABC”ÄÍâœÓÔČŁŹMÊÇBCŃÓł€ÏßÉÏÒ»”㣏ÁŹœÓAMœ»ĄŃOÓÚ”ăDŁŹŃÓł€BDÖÁ”ăNŁŹÊč”ĂBN=AMŁŹÁŹœÓCNŁŹMNŁź 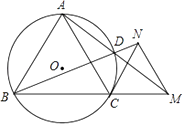
Łš1Ł©ĆĐ¶ÏĄśCMN”ÄĐÎŚŽŁŹČąÖ€ĂśÄă”ÄœáÂÛŁ»
Łš2Ł©ÇóÖ€ŁșCNÊÇĄŃO”ÄÇĐÏߣ»
Łš3Ł©Èô”È±ßĄśABC”ı߳€ÊÇ2ŁŹÇóADAM”ÄÖ”Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłÊĐ2012~2016ÄêłŁŚĄÈËżÚÊęÍłŒÆÈçÍŒËùÊŸĄŁ
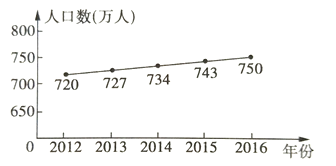
Łš1Ł©žĂÊĐłŁŚĄÈËżÚÊę2016Äê±È2015ÄêÔöŒÓÁË___________ÍòÈËŁ»
Łš2Ł©ÓëÉÏÒ»ÄêÏà±ÈŁŹžĂÊĐłŁŚĄÈËżÚÊęÔöł€ÂÊŚîŽó”ÄÄê·ĘÊÇ__________________Ł»
Łš3Ł©Ô€Čâ2017ÄêžĂÊĐłŁŚĄÈËżÚŽóÔŒÓжàÉÙÍòÈËŁŹČąÓĂËùѧ”ÄÍłŒÆÖȘÊ¶Ë”ĂśÀíÓÉĄŁ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹABÊÇĄŃO”ÄÖ±Ÿ¶ŁŹCÊÇĄŃOÉÏÒ»”㣏CDĄÍABÓÚDŁŹÇÒAB=8ŁŹDB=2Łź 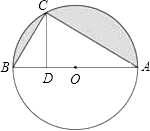
Łš1Ł©ÇóÖ€ŁșĄśABCĄŚĄśACDŁ»
Łš2Ł©ÇóÍŒÖĐÒőÓ°Čż·Ö”ÄĂæ»ęŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎÒĂÇŃ§Ï°ÁËčŽčɶšÀíș󣏶ŒÖȘ”ÀĄ°čŽÈꥹčÉËÄĄąÏÒÎ楱.
čÛČìŁș3ŁŹ4ŁŹ5Ł»5ŁŹ12ŁŹ13Ł»7ŁŹ24ŁŹ25Ł»9ŁŹ40ŁŹ41Ł»ĄĄ·ąÏÖŐâĐ©čŽčÉÊę”Ä莶ŒÊÇÆæÊ꣏ÇÒŽÓ3ÆđŸÍĂ»ÓĐŒä¶Ïčę.
Łš1Ł©ÇëÄăžùŸĘÉÏÊö”ÄčæÂÉĐŽłöÏÂÒ»ŚéčŽčÉÊęŁș_______________________Ł»
Łš2Ł©Èô”ÚÒ»žöÊęÓĂŚÖÄžnŁšnÎȘÆæÊ꣏ÇÒnĄĘ3Ł©±íÊŸŁŹÔòșóÁœžöÊęÓĂșŹn”ÄŽúÊęÊœ±íÊŸ·Ö±đÎȘ___________________ĄŁ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłč«Ô°”ÄĂĆƱŒÛžńÊÇŁșłÉÈË20ÔȘ/ŐĆŁŹŃ§Éú10ÔȘ/ŐĆŁŹÂú40ÈËżÉčșÂòÍĆÌćƱŁšÆ±ŒÛŸùŽò°ËŐÛŁ©.ÉèÒ»žöčČÓĐxÈË”ÄÂĂÓÎÍĆÈ„žĂč«Ô°ÓÎÍæŁŹÆäÖĐѧÉúÓĐyÈË.
Łš1Ł©ÓĂșŹxŁŹy”ÄÊœŚÓ±íÊŸžĂÂĂÓÎÍĆÓŠž¶”ÄĂĆƱ·ŃŁ»
Łš2Ł©ÈçčûÂĂÓÎÍĆÓĐ47ÈËŁŹÆäÖĐѧÉúÓĐ12ÈËŁŹÄÇĂŽËûĂÇÓŠž¶¶àÉÙÔȘĂĆƱ·ŃŁż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŚű±êÆœĂæÉÏŁŹÄł¶țŽÎșŻÊęÍŒĐΔĶ„”ăÎȘŁš2ŁŹ©1Ł©ŁŹŽËșŻÊęÍŒĐÎÓëxÖáÏàœ»ÓÚPĄąQÁœ”㣏ÇÒPQ=6ŁźÈôŽËșŻÊęÍŒĐÎÍšč꣚1ŁŹaŁ©ĄąŁš3ŁŹbŁ©ĄąŁš©1ŁŹcŁ©ĄąŁš©3ŁŹdŁ©ËĔ㣏ÔòaĄąbĄącĄądÖźÖ”șÎŐßÎȘŐꣿŁšĄĄĄĄŁ©
A.a
B.b
C.c
D.d
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłÊĐÔÚłÇÖĐŽćžÄÔìÖĐŁŹĐèÒȘÖÖÖČ![]() Ąą
Ąą![]() ÁœÖÖȻ͏”ÄÊśĂçčČ
ÁœÖÖȻ͏”ÄÊśĂçčČ![]() żĂŁŹŸŐĐ±êŁŹłĐ°üÉÌÒÔ
żĂŁŹŸŐĐ±êŁŹłĐ°üÉÌÒÔ![]() ÍòÔȘ”ıšŒÛÖбêłĐ°üÁËŐâÏîč€łÌŁŹžùŸĘ”śČ錰ÏàčŰŚÊÁϱíĂśŁŹ
ÍòÔȘ”ıšŒÛÖбêłĐ°üÁËŐâÏîč€łÌŁŹžùŸĘ”śČ錰ÏàčŰŚÊÁϱíĂśŁŹ ![]() Ąą
Ąą![]() ÁœÖÖÊśĂç”ijɱŸŒÛŒ°łÉ»îÂÊÈç±íŁș
ÁœÖÖÊśĂç”ijɱŸŒÛŒ°łÉ»îÂÊÈç±íŁș
Æ·ÖÖ | čșÂòŒÛŁšÔȘ/żĂŁ© | łÉ»îÂÊ |
|
|
|
|
|
|
ÉèÖÖÖČ![]() ÖÖÊśĂç
ÖÖÊśĂç![]() żĂŁŹłĐ°üÉÌ»ń”Ă”ÄÀûÈóÎȘ
żĂŁŹłĐ°üÉÌ»ń”Ă”ÄÀûÈóÎȘ![]() ÔȘŁź
ÔȘŁź
Łš![]() Ł©Çó
Ł©Çó![]() Óë
Óë![]() ÖźŒä”ÄșŻÊęčŰϔʜŁź
ÖźŒä”ÄșŻÊęčŰϔʜŁź
Łš![]() Ł©ŐțžźÒȘÇóÔÔÖČŐâĆúÊśĂç”ijɻîÂÊČ»”ÍÓÚ
Ł©ŐțžźÒȘÇóÔÔÖČŐâĆúÊśĂç”ijɻîÂÊČ»”ÍÓÚ![]() ŁŹłĐ°üÉÌÓŠÈçșÎŃĄÖÖÊśĂçČĆÄÜ»ń”ĂŚîŽóÀûÈ󣿌îŽóÀûÈóÊǶàÉÙŁż
ŁŹłĐ°üÉÌÓŠÈçșÎŃĄÖÖÊśĂçČĆÄÜ»ń”ĂŚîŽóÀûÈ󣿌îŽóÀûÈóÊǶàÉÙŁż
Č鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com