
����Ŀ���ۺ���ʵ��
Ԫ���ڼ䣬���и����̳��������������мס��ҡ��������̳���չ�Ĵ���������ʾ:
�̳� | �Żݻ |
�� | ȫ������۵� |
�� | ʵ�С��� (��:�˿��·� |
�� | ʵ�С��� |
�������ϻ��Ϣ�������������:
(1)���� �̳�ͬʱ����һ�����![]() Ԫ�����º�һ�����
Ԫ�����º�һ�����![]() Ԫ�Ŀ���,������������һ���·�����Ӧ��ѡ���ļ��̳�������?
Ԫ�Ŀ���,������������һ���·�����Ӧ��ѡ���ļ��̳�������?
(2)�� ���������ڼס����̳�ͬʱ����һ�����![]() Ԫ�����º�һ�����
Ԫ�����º�һ�����![]() ��Ԫ�Ŀ��ӣ����Ҳһ���������������ӵı���Ƕ���Ԫ?
��Ԫ�Ŀ��ӣ����Ҳһ���������������ӵı���Ƕ���Ԫ?
(3)���̳����Ƴ� ���ȴ��ۡ���������![]() ��
��![]() Ԫ���Ļ������������һ�����Ϊ
Ԫ���Ļ������������һ�����Ϊ![]() Ԫ�����£����������־�Ȼ��û����ǰ�ึ��
Ԫ�����£����������־�Ȼ��û����ǰ�ึ��![]() ԪǮ���ʱ��̳��ȴ��˶����ۺ��ٲμӻ?
ԪǮ���ʱ��̳��ȴ��˶����ۺ��ٲμӻ?
���𰸡���1��ѡ����̳Ǹ�����. ��2��370Ԫ. ��3��9.5��
��������
��1�����ղ�ͬ���Żݷ�����������̳�ʵ�ʻ���Ǯ�����ٱȽϵó��𰸼��ɣ�
��2�����������ӵı��ΪxԪ�������Żݷ������ʵ�ʸ����������ݸ����һ�����з�����⼴�ɣ�
��3��������̳��ȴ���n�ۺ��ٲμӻ�����ݴ��ۺ��û����ǰ�ึ��18.5ԪǮ���з�����⣮
��1��ѡ���̳��踶����Ϊ��290+270����0.6=336��Ԫ����
ѡ���̳��踶����Ϊ290+��270-200��=360��Ԫ����
ѡ���̳��踶����Ϊ290+270-5��50=310��Ԫ����
��360��336��310��
��ѡ����̳������㣮
��2�����������ӵı��ΪxԪ��
����������380+x����0.6=380+x-100��3��
��ã�x=370��
���������ӵı��Ϊ370Ԫ��
��3������̳��ȴ���n�ۺ��ٲμӻ����������ɵô��ۺ�ļ۸�С��600Ԫ����С��500Ԫ��
����������630��![]() -5��50��-��630-6��50��=18.5
-5��50��-��630-6��50��=18.5
���n=9.5
�𣺱��̳��ȴ���9.5�ۺ��ٲμӻ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij������ʻ��·��S(km)��ʱ��t(min)�ĺ�����ϵͼ���۲�ͼ�����ṩ����Ϣ������������⣺
��1��������ǰ9�����ڵ�ƽ���ٶ��Ƕ��٣�
��2����������;ͣ�˶ʱ�䣿
��3����16��t��30ʱ����S��t�ĺ�����ϵʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
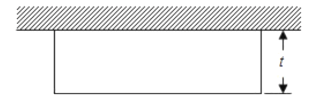
����Ŀ���г�Ϊl����ʣ��������ͷ��ݵ�һ��ǽΧ����ͼ��״���ӣ��ӵĿ�Ϊt��
��1���ù���l��t�Ĵ���ʽ��ʾ�ӵ�������������ʽ�Ƕ���ʽ���ǵ���ʽ��
��2����l��100�̶����䣬��t��ֵȡ20��25��30ʱ������һ��ȡ����Χ�ɵ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
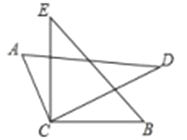
����Ŀ����һ�����ǰ��е�������ͼ��ʾ�ķ�ʽ������һ��ֱ�Ƕ����غϣ�
��1����![]() ʱ����
ʱ����![]() �Ķ�����
�Ķ�����
��2����![]() ƽ��
ƽ��![]() ʱ����
ʱ����![]() �Ķ�������д��������̣���
�Ķ�������д��������̣���
��3�����벢ֱ��д��![]() ��
��![]() ��������ϵ������˵�����ɣ���
��������ϵ������˵�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̳�ij����Ʒƽ��ÿ�������30����ÿ��ӯ��50Ԫ��Ϊ�˾�����ٿ�棬�̳�������ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣�ÿ����Ʒÿ����1Ԫ���̳�ƽ��ÿ��ɶ��۳�2������ÿ����Ʒ����![]() Ԫ���ݴ˹��ɣ���ش�
Ԫ���ݴ˹��ɣ���ش�
��1���̳�������������_____����ÿ����Ʒӯ��_____Ԫ���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2���������������䡢������������£�ÿ����Ʒ���۶���Ԫʱ���̳���ӯ���ɴﵽ2100Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
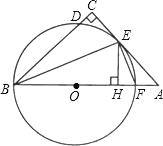
����Ŀ����ͼ������ABC�У���C=90������ABC��ƽ���߽�AC�ڵ�E������E��BE�Ĵ��߽�AB�ڵ�F����O����BEF�����Բ��
��1����֤��AC����O�����ߣ�
��2������E��EH��AB������ΪH����֤��CD=HF��
��3����CD=1��EH=3����BF��AF����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
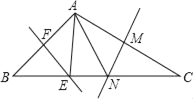
����Ŀ����ͼ��ʾ���ڡ�ABC�У���BAC=106�㣬EF��MN�ֱ���AB��AC�Ĵ�ֱƽ���ߣ���E��N��BC�ϣ����EAN=_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�С�����о���ѧ����ʱ����һ�����壺�����ź�˳�����������x1��x2��x3����Ϊ����x1��x2��x3������![]() ��
��![]() ��
��![]() ����������������Сֵ��Ϊ����x1��x2��x3�ļ�ֵ.���磬��������2��-1��3����Ϊ
����������������Сֵ��Ϊ����x1��x2��x3�ļ�ֵ.���磬��������2��-1��3����Ϊ![]() ��
��![]() ��
��![]() ����������2��-1��3�ļ�ֵΪ
����������2��-1��3�ļ�ֵΪ![]() .
.
С����һ�����֣����ı�����������˳��ʱ�����õ������ж�����������������������Ӧ�ļ�ֵ.������-1��2��3�ļ�ֵΪ![]() ������3��-1��2�ļ�ֵΪ1���������о���С�����֣�������2��-1��3���������������ղ�ͬ������˳��õ��IJ�ͬ�����У���ֵ����СֵΪ
������3��-1��2�ļ�ֵΪ1���������о���С�����֣�������2��-1��3���������������ղ�ͬ������˳��õ��IJ�ͬ�����У���ֵ����СֵΪ![]() .�������ϲ��ϣ��ش��������⣺
.�������ϲ��ϣ��ش��������⣺
(1)����4��3��-2�ļ�ֵΪ______.
(2)����4��3��-2�������������ղ�ͬ��˳�����У��ɵõ����ɸ����У�����Щ���еļ�ֵ����Сֵ(��д�����̲�����).
(3)��3��-8��a(a>1)�����������ղ�ͬ��˳�����У��ɵõ����ɸ�����.����Щ���еļ�ֵ����СֵΪ1����a��ֵΪ_______ (ֱ��д����).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
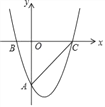
����Ŀ����ͼ��������y=![]() x2+bx+c����A��0����6����B����2��0������x�����һ����Ϊ��C��
x2+bx+c����A��0����6����B����2��0������x�����һ����Ϊ��C��
��1����������ߵĽ���ʽ��
��2����ֱ��AC����ƽ��m����λ��ʹƽ�ƺ��ֱ��������������ֻ��һ��������M����m��ֵ����M�����ꣻ
��3�����������Ƿ���ڵ�P��ʹ��PACΪֱ�������Σ������ڣ���ֱ��д����P�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com