
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过B(3,0),C(0,-3)两点,点D为顶点.
经过B(3,0),C(0,-3)两点,点D为顶点.
(1)求抛物线的解析式及顶点D的坐标;
(2)点E在抛物线的对称轴上,F在BD上,求BE+EF的最小值;
(3)点P是抛物线第四象限的点(不与B、C重合),连接PB,以PB为边作正方形BPMN,当点M或N恰好落在对称轴上时,求出对应的P点的坐标(结果保留根号).

【答案】(1)![]() ,D(1,-4);(2)
,D(1,-4);(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)把B、C点的坐标代入抛物线方程,利用待定系数法,可以把方程中的未知数求解出来,从而得到抛物线的表达式,把解析式整理成顶点式,即可得到顶点D的坐标;
(2)利用对称轴的性质,知道AE=BE,从而把BE+EF的长度转换成AF的长度,求出BE+EF的最小值;
(3)利用全等三角形的性质,根据已知线段可求得相应坐标.
解:(1)把B、C点的坐标代入抛物线方程得到:
![]()
解得![]()
∴表达式为![]() ,
,
又∵![]() ,
,
所以顶点的坐标为D(1,-4),
(2)如图1,连接BD,过A作AF⊥BD于F,交对称轴于点E,
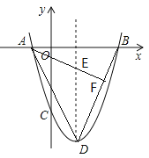
图1
∵E点在抛物线的对称轴上
∴AE=BE
则BE+EF=AE+EF=AF
又因为两点之间垂线段最短
所以所做的AF为所求的最小值
由三角形的面积公式可以得到 ![]() (h是三角形ABD以AB为边的高)
(h是三角形ABD以AB为边的高)
又由题意可知![]() ,
,![]() ,
,![]()
所以![]() ,
,
因此:![]() ,
,
∴BE+EF的最小值为![]() .
.
(3)当点N在对称轴上时,如图2,过点P作PF⊥OB于点F,
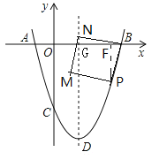
图2
∵四边形PBNM是正方形 , ∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
在和
![]() 中
中
∵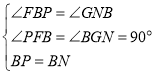
∴![]() (AAS),
(AAS),
∴ ![]() ,
,
设点P的坐标为(![]() ),则
),则![]() ,整理得
,整理得![]()
解得:![]() ,
,![]() (舍去)
(舍去)
∴![]()
当点M在对称轴上时,如图3,过点P作PG⊥OB于点G,过点P作PF⊥MD于点F,
同理可证:![]() ,∴
,∴![]()
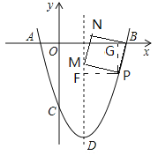
图3
设![]() ,代入得
,代入得![]() ,
,
解得:![]() ,
,![]() (舍去)
(舍去)
当![]() 时,
时,![]() ,
,![]()
综上所述:对应的P点的坐标有![]() 或
或![]()


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
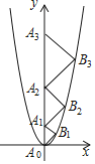
【题目】二次函数![]() 的图象如图,点
的图象如图,点![]() 位于坐标原点,点
位于坐标原点,点![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在二次函数
在二次函数![]() 位于第一象限的图象上,
位于第一象限的图象上,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 都是直角顶点在抛物线上的等腰直角三角形,则
都是直角顶点在抛物线上的等腰直角三角形,则![]() 的斜边长为________.
的斜边长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.
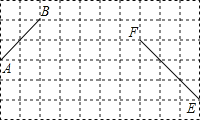
(1)在图中以AB为边画Rt△BAC,点C在小正方形的顶点上,使∠BAC=90°,tan∠ACB=![]() ;
;
(2)在(1)的条件下,在图中画以EF为边且面积为3的△DEF,点D在小正方形的顶点上,连接CD、BD,使△BDC是锐角等腰三角形,直接写出∠DBC的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格图中建立平面直角坐标系,![]() 的顶点坐标为
的顶点坐标为![]() 、
、![]() 、
、![]() .
.
(1)若将![]() 向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的
向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的![]() ;
;
(2)画出![]() 绕C1顺时针方向旋转90°后得到的
绕C1顺时针方向旋转90°后得到的![]() ;
;
(3)![]() 与
与![]() 是中心对称图形,请写出对称中心的坐标: ;并计算
是中心对称图形,请写出对称中心的坐标: ;并计算![]() 的面积: .
的面积: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为构建“魅力雨花,和谐雨花,人文雨花”,规划在圭塘河上修建一座观光人行桥(如图1),此工程由桥梁工程与桥上拱形工程组成,桥上拱形工程包含三组完全相同的拱形,观光人行桥的正规图如图2所示,已知桥面上三组拱桥都为相同的抛物线![]() 的一部分,拱高(抛物线最高点到桥面的距离)为16米,三条抛物线依次与桥面AB相较于点A,C,D,B.
的一部分,拱高(抛物线最高点到桥面的距离)为16米,三条抛物线依次与桥面AB相较于点A,C,D,B.

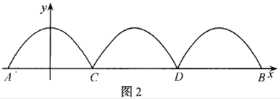
(1)求桥长AB;
(2)已知一组桥拱的造价为a万元,桥面每米的平均造价为b万元.若一组桥拱的造价为整个桥面造价的![]() ,这座观光桥的总造价为504万元,求a,b的值.
,这座观光桥的总造价为504万元,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
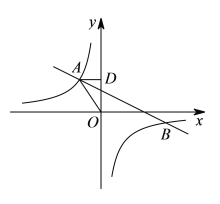
【题目】如图,在平面直角坐标系中,反比例函数![]()
![]() 与一次函数
与一次函数![]() 交于第二、四象限的
交于第二、四象限的![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)请根据图象直接写出![]() 的自变量
的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,折叠正方形纸片,使
,折叠正方形纸片,使![]() 落在
落在![]() 上,点
上,点![]() 恰好与
恰好与![]() 上的点
上的点![]() 重合,展开后折痕
重合,展开后折痕![]() 分别交
分别交![]() 于点
于点![]() ,连
,连![]() 给出下列结论,其中正确的个数有( )
给出下列结论,其中正确的个数有( )
①![]() ;②
;②![]() ;③四边形
;③四边形![]() 是菱形;④
是菱形;④![]() .
.
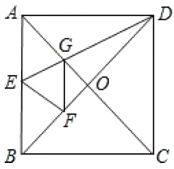
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com