
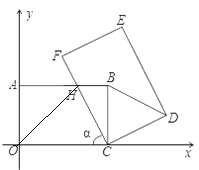
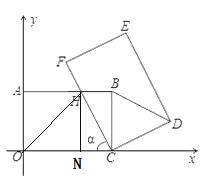
【题目】如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB交于点H,且A(0,3),C(5,0).
(1)当α=60°时,△CBD的形状是 _________ ;
(2)当0°<α<90°旋转过程中,连结OH,当△OHC为等腰三角形时,请直接写出点H的坐标.

【答案】等边三角形
【解析】分析:(1)根据旋转的性质可得BC=CD,∠BCD=∠α=60°,根据有一个角为60°的等腰三角形为等边三角形,即可得△BCD是等边三角形;(2)分OH=OC,OH=HC,OC=CH三种情况求点H的坐标.
详解:
(1)∵图形旋转后BC=CD,∠BCD=∠α=60°,
∴△BCD是等边三角形;
(2)当OH=OC时,
∵C(5,0),
∴OC=OH=5.
在Rt△AOH中,根据勾股定理求得AH=4,
∴H(4,3);
当OH=HC时,
过点H作HN垂直于OC于点N,根据等腰三角形的三线合一的性质可得OM=MC=2.5,
∴H(2.5,3);

当OC=HC时,
过点H作HM垂直于OC于点M,
在Rt△AOH中,根据勾股定理求得CN=4,
∴ON=OC-CN=5-4=1,
∴H(1,3);
综上,H点的坐标是(1,3),(2.5,3),(4,3).


科目:初中数学 来源: 题型:
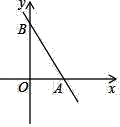
【题目】如图,直线y=﹣![]() x+4
x+4![]() 分别与x轴,y轴相交于点A,B,点C在直线AB上,D是坐标平面内一点,若以点O,A,C,D为顶点的四边形是菱形,则点D的坐标是_____.
分别与x轴,y轴相交于点A,B,点C在直线AB上,D是坐标平面内一点,若以点O,A,C,D为顶点的四边形是菱形,则点D的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
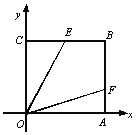
【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2![]() ,若∠EOF=45°,则F点的纵坐标是( )
,若∠EOF=45°,则F点的纵坐标是( )
A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得元购物券,至多可得元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段BD、CE交于点M.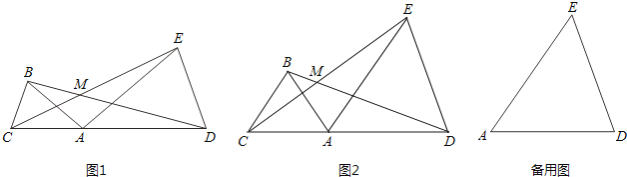
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;
②求∠BMC的大小(用α表示);
(2)如图2,若AB=BC=kAC,AD=ED=kAE,则线段BD与CE的数量关系为 , ∠BMC=(用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接EC并延长交BD于点M.则∠BMC=(用α表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各数填入相应的集合中:
—7 , 0,![]() , —2.55555……, 3.01, +9 , 4.020020002…, +10﹪,
, —2.55555……, 3.01, +9 , 4.020020002…, +10﹪, ![]()
有理数集合:{ };
无理数集合:{ };
整数集合:{ };
分数集合:{ }
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:一粒米微不足道,平时在饭桌上总会毫不经意地掉下几粒,甚至有些挑食的同学把整碗米饭倒掉.针对这种浪费粮食现象,老师组织同学们进行了实际测算,称得![]() 粒大米约重
粒大米约重![]() 克.
克.
尝试解决:
![]() 粒米重约多少克?
粒米重约多少克?
![]() 按我国现有人口
按我国现有人口![]() 亿,每年
亿,每年![]() 天,每人每天三餐计算,若每人每餐节约
天,每人每天三餐计算,若每人每餐节约![]() 粒大米,一年大约能节约大米多少千克?(结果用科学记数法表示)
粒大米,一年大约能节约大米多少千克?(结果用科学记数法表示)
![]() 假设我们把一年节约的大米卖成钱,按每千克
假设我们把一年节约的大米卖成钱,按每千克![]() 元计算,可卖得人民币多少元?(结果用科学记数法表示,保留到
元计算,可卖得人民币多少元?(结果用科学记数法表示,保留到![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解本校学生对球类运动的爱好情况,采用抽样的方法,从乒乓球、羽毛球、篮球和排球四个方面调查了若干名学生,在还没有绘制成功的“折线统计图”与“扇形统计图”中,请你根据已提供的部分信息解答下列问题. 
(1)在这次调查活动中,一共调查了名学生,并请补全统计图.
(2)“羽毛球”所在的扇形的圆心角是度.
(3)若该校有学生1200名,估计爱好乒乓球运动的约有多少名学生?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com