
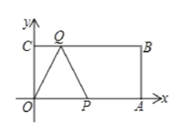
【题目】如图,矩形OABC的边OA在x轴上,OA=10cm,OC在y轴上,且OC=4cm,P为OA 的中点,动点Q从C点出发,沿着CB以每秒1cm的速度运动(Q到B点时停止运动),当△OPQ是以OP为腰的等腰三角形时,点Q的运动时间=_______.
科目:初中数学 来源: 题型:
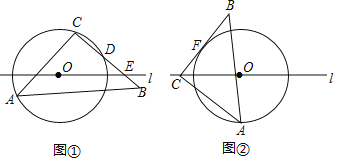
【题目】已知,△ABC中,∠ACB=90°,AC=BC=8,点A在半径为5的⊙O上,点O在直线l上.
(1)如图①,若⊙O经过点C,交BC于点D,求CD的长.
(2)在(1)的条件下,若BC边交l于点E,OE=2![]() ,求BE的长.
,求BE的长.
(3)如图②,若直线l还经过点C,BC是⊙O 的切线,F为切点,则CF的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
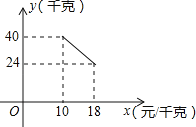
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(3,y2)是抛物线上两点,则y1<y2,其中说法正确的是( )
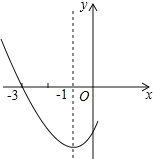
A.①②B.②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接 AC、OD交于点E.
(1)若tan∠ABC=2,证明:DA与⊙O相切:
(2)在(1)条件下,连接BD交⊙O于点F,连接EF,若BC=1,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
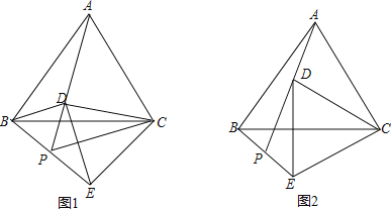
【题目】已知:△ABC是等边三角形,点D是△ABC(包含边界)平面内一点,连接CD,将线段CD绕C逆时针旋转60°得到线段CE,连接BE,DE,AD,并延长AD交BE于点P.
(1)观察填空:当点D在图1所示的位置时,填空:
①与△ACD全等的三角形是______.
②∠APB的度数为______.
(2)猜想证明:在图1中,猜想线段PD,PE,PC之间有什么数量关系?并证明你的猜想.
(3)拓展应用:如图2,当△ABC边长为4,AD=2时,请直接写出线段CE的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com