
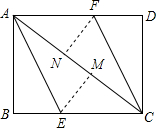
 如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.分析 (1)首先由矩形的性质和折叠的性质证得AB=CD,AD∥BC,∠ANF=90°,∠CME=90°,易得AN=CM,可得△ANF≌△CME(ASA),由平行四边形的判定定理可得结论;
(2)由AB=6,AC=10,可得BC=8,设CE=x,则EM=8-x,CM=10-6=4,在Rt△CEM中,利用勾股定理可解得x,由平行四边形的面积公式可得结果.
解答 (1)证明:∵折叠,
∴AM=AB,CN=CD,∠FNC=∠D=90°,∠AME=∠B=90°,
∴∠ANF=90°,∠CME=90°,
∵四边形ABCD为矩形,
∴AB=CD,AD∥BC,
∴AM=CN,
∴AM-MN=CN-MN,
即AN=CM,
在△ANF和△CME中,
$\left\{\begin{array}{l}{∠FAN=∠ECM}\\{AN=CM}\\{∠ANF=∠CME}\end{array}\right.$,
∴△ANF≌△CME(ASA),
∴AF=CE,
又∵AF∥CE,
∴四边形AECF是平行四边形;
(2)解:∵AB=6,AC=10,∴BC=8,
设CE=x,则EM=8-x,CM=10-6=4,
在Rt△CEM中,
(8-x)2+42=x2,
解得:x=5,
∴四边形AECF的面积的面积为:EC•AB=5×6=30.
点评 本题主要考查了折叠的性质、矩形的性质、平行四边形的判定定理和勾股定理等,综合运用各定理是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )| A. | 2$\sqrt{2}$<r≤$\sqrt{17}$ | B. | $\sqrt{17}$<r≤3$\sqrt{2}$ | C. | $\sqrt{17}$<r≤5 | D. | 5<r≤$\sqrt{29}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(岁) | 18 | 19 | 20 | 21 | 22 |
| 人数 | 2 | 5 | 2 | 2 | 1 |
| A. | 2,20岁 | B. | 2,19岁 | C. | 19岁,20岁 | D. | 19岁,19岁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com