
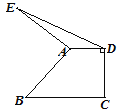
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于 ( )
A.10 B.11 C.12 D.13
科目:初中数学 来源: 题型:
【题目】有下列命题:①对顶角相等;②若a∥b,b∥c,则a∥c;③在同一平面内,若a⊥b,b⊥c,则a∥c;④ac=bc,则a=b.其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.
(1)若∠AOB=60°,AB∥x轴,AB=2,求a的值;
(2)若∠AOB=90°,点A的横坐标为﹣4,AC=4BC,求点B的坐标;
(3)延长AD、BO相交于点E,求证:DE=CO.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为⊙
为⊙![]() 上一点,点
上一点,点![]() 在直径
在直径![]() 的延长线上,且
的延长线上,且![]() .
.
(1)判断直线![]() 和⊙
和⊙![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(2)过点![]() 作⊙
作⊙![]() 的切线
的切线![]() 交直线
交直线![]() 于点
于点![]() ,若
,若![]() ,⊙
,⊙![]() 的半径是
的半径是![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.正数和负数统称为有理数
B.0是最小的有理数
C.如果两个数的绝对值相等,那么这两个数一定相等
D.互为相反数的两个数之和为零
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇正在建造的文化广场工地上,有两种铺设广场地面的材料,一种是长为![]() cm,宽为
cm,宽为![]() cm的长方形板材(如图),另一种是边长为
cm的长方形板材(如图),另一种是边长为![]() cm的正方形地砖(如图②)
cm的正方形地砖(如图②)

(1)用几块如图②所示的正方形地砖能拼出一个新的正方形?并写出新正方形的面积
(写出一个符合条件的答案即可);
(2)我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问
题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一,所谓“作差
法”:就是通过作差、变形,并利用差的符号来确定它们的大小,即要比较代数式M、
N的大小,只要作出它们的差![]() ,若
,若![]() ,则
,则![]() ;若
;若![]() ,则
,则
![]() ;若
;若![]() ,则
,则![]() .
.
请你用“作差法”解决以下问题:用如图①所示的四块长方形板材铺成如图③的大正方形或如图④的大长方形,中间分别空出一个小正方形和小长方形(图中阴影部分);
① 请用含![]() 、
、![]() 的代数式分别表示图③和图④中阴影部分的面积;
的代数式分别表示图③和图④中阴影部分的面积;
② 试比较图③和图④中阴影部分的面积哪个大?大多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com