
【题目】如图,![]() 为直线
为直线![]() 上一点,
上一点,![]() 平分
平分![]() ,则以下结论正确的有______.(只填序号)①
,则以下结论正确的有______.(只填序号)①![]() 与
与![]() 互为余角;②若
互为余角;②若![]() ,则
,则![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() .
.

【答案】①②③
【解析】
由平角的定义与∠DOE=90°,即可求得∠AOD与∠BOE互为余角;又由角平分线的定义,可得∠AOE=2∠COE=2∠AOC,根据余角和补角的定义可得∠BOE=2∠COD,根据角平分线的定义和补角的定义可得若∠BOE=58°,则∠COE=61°.
∵∠DOE=90°,
∴∠COD+∠COE=90°,∠EOB+∠DOA=90°,
即∠AOD与∠BOE互为余角,
故①正确;
∵OC平分∠AOE,
∴∠AOE=2∠COE=2∠AOC;
∵∠BOE=180°﹣2∠COE,
∴∠COD=90°﹣∠COE,
∴∠BOE=2∠COD,
故③正确;
若∠BOE=58°.
∵∠AOE+∠BOE=180°,
∴∠COE![]() (180°﹣∠BOE)=61°,
(180°﹣∠BOE)=61°,
故②正确;
没有条件能证明OD平分∠COA,故④错误.
综上所述:正确的有①②③.
故答案为:①②③.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
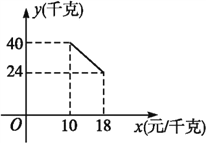
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得168元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
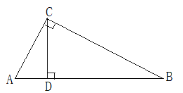
【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.
(1)求△ABC的面积;
(2)求CD的长;
(3)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(4)作出△BCD的边BC上的高DF,当BD=![]() 时,试求出DF的长(用
时,试求出DF的长(用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建筑工地计划租用甲、乙两辆车清理建筑垃圾,已知甲车单独运完需要15天,乙车单独运完需要30天.甲车先运了3天,然后甲、乙两车合作运完剩下的垃圾.
(1)甲、乙两车合作还需要多少天运完垃圾?
(2)已知甲车每天的租金比乙车多100元,运完垃圾后建筑工地共需支付租金3950元.则甲、乙车每天的租金分别为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知双曲线![]() 与直线
与直线![]() 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线![]() 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线![]() 于点E,交BD于点C.
于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明到小陈家所在的美丽乡村游玩,在村头A处小明接到小陈发来的定位,发现小陈家C在自己的北偏东45°方向,于是沿河边笔直的绿道l步行200米到达B处,这时定位显示小陈家C在自己的北偏东30°方向,如图所示,根据以上信息和下面的对话,请你帮小明算一算他还需沿绿道继续直走多少米才能到达桥头D处(精确到1米)(备用数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设国家森林城市,园林部门决定搭配A.B两种园艺造型共50个摆放在市区,现有3490盆甲种花卉和2950盆乙种花卉可供使用,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个A种造型的费用是800元,搭配一个B种造型的费用是960元,试说明(1)中哪种方案费用最低?最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC∥GE,AF∥DE,∠1=50°.
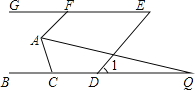
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
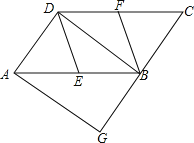
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com