
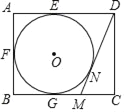
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于点E、F、G,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
【答案】B
【解析】
连接OE,OF,ON,OG,在矩形ABCD中,得到∠A=∠B=90°,CD=AB=4,由于AD,AB,BC分别与⊙O相切于E,F,G三点,得到∠AEO=∠AFO=∠OFB=∠BGO=90°,推出四边形AFOE,FBGO是正方形,得到AF=BF=AE=BG=2,然后由勾股定理列方程即可求出DM.
解:连接OE,OF,ON,OG,
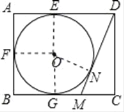
在矩形ABCD中,
∵∠A=∠B=90°,CD=AB=4,
∵AD,AB,BC分别与⊙O相切于E,F,G三点,
∴∠AEO=∠AFO=∠OFB=∠BGO=90°,
∴四边形AFOE,FBGO是正方形,
∴AF=BF=AE=BG=2,
∴DE=3,
∵DM是⊙O的切线,
∴DN=DE=3,MN=MG,
∴CM=5﹣2﹣MN=3﹣MN,
在Rt△DMC中,DM2=CD2+CM2,
∴(3+NM)2=(3﹣NM)2+42,
∴NM=![]() ,
,
∴DM=3+![]() =
=![]() .
.
故本题答案为:B.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
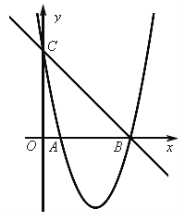
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(x1,y1)、B(x2,y2)都在某函数图象上,且当x1<x2<0时,y1>y2,则此函数一定不是( )
A. ![]() B. y=﹣2x+1 C. y=x2﹣1 D.
B. y=﹣2x+1 C. y=x2﹣1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6cm,BC=7cm,∠ABC=30°,点P从A点出发,以1cm/s的速度向B点移动,点Q从B点出发,以2cm/s的速度向C点移动.如果P、Q两点同时出发,经过几秒后△PBQ的面积等于4cm2?
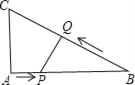
查看答案和解析>>
科目:初中数学 来源: 题型:
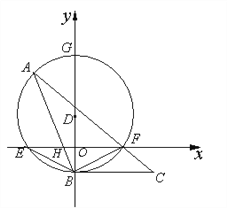
【题目】如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在![]() 上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
(1)判断直线BC与⊙D的位置关系,并说明理由;
(2)求证:BE2=BH·AB;
(3) 若点E坐标为(-4,0),点B的坐标为(0,-2),AB=8,求F与A两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
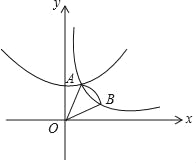
【题目】如图,已知反比例函数y=![]() (x>0)的图象绕原点O逆时针旋转45°,所得的图象与原图象相交于点A,连接OA,以O为圆心,OA为半径作圆,交函数y=
(x>0)的图象绕原点O逆时针旋转45°,所得的图象与原图象相交于点A,连接OA,以O为圆心,OA为半径作圆,交函数y=![]() (x>0)的图象与点B,则扇形AOB的面积为_____.
(x>0)的图象与点B,则扇形AOB的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
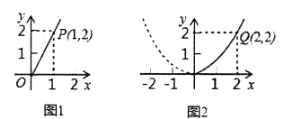
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资金额
与投资金额![]() 成正比例关系,如图1所示;种植花卉的利润
成正比例关系,如图1所示;种植花卉的利润![]() 与投资金额
与投资金额![]() 成二次函数关系,如图2所示.(注:利润与投资金额的单位均为万元)
成二次函数关系,如图2所示.(注:利润与投资金额的单位均为万元)
(1)分别求出利润![]() 与
与![]() 关于投资金额
关于投资金额![]() 的函数关系;
的函数关系;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉的金额是![]() 万元,求这位专业户能获取的最大总利润是多少万元?
万元,求这位专业户能获取的最大总利润是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com