
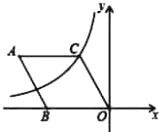
【题目】如图,在菱形ABOC中,AB=2,∠A=60°,菱形的一个顶点C在反比例函数y=![]() (k≠0)的图象上,则反比例函数的解析式为( )
(k≠0)的图象上,则反比例函数的解析式为( )
A.y=![]() B.y=
B.y=![]() C.y=
C.y=![]() D.y=
D.y=![]()
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天,求甲、乙两厂每天能生产口罩多少万只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条公路上顺次有A、B、C三地,甲、乙两车同时从A地出发,分别匀速前往B地、C地,甲车到达B地停留一段时间后原速原路返回,乙车到达C地后立即原速原路返回,乙车比甲车早1小时返回A地,甲、乙两车各自行驶的路程y(千米)与时间x(时)(从两车出发时开始计时)之间的函数图象如图所示.
(1)甲车到达B地停留的时长为 小时.
(2)求甲车返回A地途中y与x之间的函数关系式.
(3)直接写出两车在途中相遇时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情爆发之后,全国许多省市对湖北各地进行了援助,广州市某医疗队备好医疗防护物资迅速援助武汉.第一批医疗队员乘坐高铁从广州出发,2.5小时后,第二批医疗队员乘坐飞机从广州出发,两批队员刚好同时到达武汉.已知广州到武汉的飞行距离为800千米,高铁路程为飞行距离的![]() 倍.
倍.
(1)求广州到武汉的高铁路程;
(2)若飞机速度与高铁速度之比为5:2,求飞机和高铁的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场打算在年前用30000元购进一批彩灯进行销售,由于进货厂家促销,实际可以以8折的价格购进这批彩灯,结果可以比计划多购进了100盏彩灯.
(1)该商场购进这种彩灯的实际进价为多少元?
(2)该商场打算在实际进价的基础上,每盏灯加价50%的销售,但可能会面临滞销,因此将有20%的彩灯需要降价,以5折出售,该商场要想获利不低于15000元,应至少在购进这种彩灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年是5G爆发元年,三大运营商都在政策的支持下,加快着5G建设的步伐.某通信公司实行的5G畅想套餐,部分套餐资费标准如下:
套餐类型 | 月费(元/月) | 套餐内包含内容 | 套餐外资费 | ||
国内数据流量(GB) | 国内主叫(分钟) | 国内流量 | 国内主叫 | ||
套餐1 | 128 | 30 | 200 | 每5元1GB,用满3GB后每3元1GB,不足部分按照0.03/元MB收取 | 0.19元/分钟 |
套餐2 | 158 | 40 | 300 | ||
套餐3 | 198 | 60 | 500 | ||
套餐4 | 238 | 80 | 600 | ||
小武每月大约使用国内数据流量49GB,国内主叫350分钟,若想使每月付费最少,则他应预定的套餐是( )
A.套餐1B.套餐2C.套餐3D.套餐4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定,以二次函数![]() 的二次项系数
的二次项系数![]() 的2倍为一次项系数,一次项系数
的2倍为一次项系数,一次项系数![]() 为常数项构造的一次函数
为常数项构造的一次函数![]() 叫做二次函数
叫做二次函数![]() 的“子函数”,反过来,二次函数
的“子函数”,反过来,二次函数![]() 叫做一次函数
叫做一次函数![]() 的“母函数”.
的“母函数”.
(1)若一次函数![]() 是二次函数
是二次函数![]() 的“子函数”,且二次函数经过点
的“子函数”,且二次函数经过点![]() ,求此二次函数的解析式.
,求此二次函数的解析式.
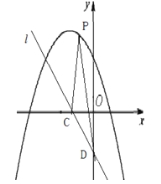
(2)如图,已知二次函数![]() 的“子函数”图象直线
的“子函数”图象直线![]() 与
与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 是直线
是直线![]() 上方的抛物线上任意一点,求
上方的抛物线上任意一点,求![]() 的面积的最大值.
的面积的最大值.
(3)已知二次函数![]() 与它的“子函数”
与它的“子函数”![]() 的函数图象有两个交点
的函数图象有两个交点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com