
【题目】如图,在直角坐标系中,△ABC的三个顶点都在坐标轴上,A,B两点关于y轴对称,点C是y轴正半轴上一个动点,AD是角平分线.
(1)如图1,若∠ACB=90°,直接写出线段AB,CD,AC之间数量关系;
(2)如图2,若AB=AC+BD,求∠ACB的度数;
(3)如图2,若∠ACB=100°,求证:AB=AD+CD.

【答案】(1)AB=AC+CD;(2)108°;(3)证明见解析
【解析】
(1)如图1,过D作DM⊥AB于M,根据轴对称的性质得到CA=CB,根据角平分线的性质得到CD=MD,∠ABC=45°,根据全等三角形的性质得到AC=AM,于是得到结论;
(2)设∠ACB=α,则∠CAB=∠CBA=90°-![]() α,在AB上截取AK=AC,连结DK,根据角平分线的定义得到∠CAD=∠KAD,根据全等三角形的性质得到∠ACD=∠AKD=α,根据三角形的内角和即可得到结论;
α,在AB上截取AK=AC,连结DK,根据角平分线的定义得到∠CAD=∠KAD,根据全等三角形的性质得到∠ACD=∠AKD=α,根据三角形的内角和即可得到结论;
(3)如图2,在AB上截取AH=AD,连接DH,根据等腰三角形的性质得到∠CAB=∠CBA=40°,根据角平分线的定义得到∠HAD=∠CAD=20°,求得∠ADH=∠AHD=80°,在AB上截取AK=AC,连接DK,根据全等三角形的性质得到∠ACB=∠AKD=100°,CD=DK,根据等腰三角形的性质得到DH=BH,于是得到结论.
(1)如图1,过D作DM⊥AB于M,
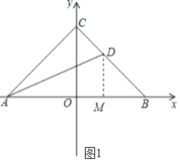
∵A,B两点关于y轴对称,
∴CA=CB,
∵∠ACB=90°,AD是角平分线,
∴CD=MD,∠ABC=45°,
∴∠BDM=45°,
∴BM=DM,
∴BM=CD,
在RT△ADC和RT△ADM中,![]() ,
,
∴RT△ADC≌RT△ADM(HL),
∴AC=AM,
∴AB=AM+BM=AC+CD,
即AB=AC+CD;
(2)设∠ACB=α,则∠CAB=∠CBA=90°﹣![]() α,
α,
在AB上截取AK=AC,连结DK,
∵AB=AC+BD,
∴BK=BD,
∵AD是角平分线,
∴在△CAD和△KAD中,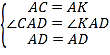 ,
,
∴△CAD≌△KAD(SAS),
∴∠ACD=∠AKD=α,
∴∠BKD=180°﹣α,
∵BK=BD,
∴∠BDK=180°﹣α,
在△BDK中,
180°﹣α+180°﹣α+90°﹣![]() α=180°,
α=180°,
∴α=108°,
∴∠ACB=108°;
(3)如图2,在AB上截取AH=AD,连接DH,
∵∠ACB=100°,AC=BC,
∴∠CAB=∠CBA=40°,
∵AD是角平分线,
∴∠HAD=∠CAD=20°,
∴∠ADH=∠AHD=80°,
在AB上截取AK=AC,连接DK,
由(1)得,△CAD≌△KAD,
∴∠ACB=∠AKD=100°,CD=DK,
∴∠DKH=80°=∠DHK,
∴DK=DH=CD,
∵∠CBA=40°,
∴∠BDH=40°,
∴DH=BH,
∴BH=CD,
∵AB=AH+BH,
∴AB=AD+CD.


科目:初中数学 来源: 题型:
【题目】某公司生产一种新型节能电水壶并加以销售,现准备在甲城市和乙城市两个不同地方按不同销售方案进行销售,以便开拓市场.
若只在甲城市销售,销售价格为![]() (元/件)、月销量为
(元/件)、月销量为![]() (件),
(件),![]() 是
是![]() 的一次函数,如表,
的一次函数,如表,
月销量 |
|
|
销售价格 |
|
|
成本为![]() 元/件,无论销售多少,每月还需支出广告费
元/件,无论销售多少,每月还需支出广告费![]() 元,设月利润为
元,设月利润为![]() (元)
(元)
(利润![]() 销售额-成本-广告费).
销售额-成本-广告费).
若只在乙城市销售,销售价格为![]() 元/件,受各种不确定因素影响,成本为
元/件,受各种不确定因素影响,成本为![]() 元/件
元/件![]() 为常数,
为常数,![]() ,当月销量为
,当月销量为![]() (件)时,每月还需缴纳
(件)时,每月还需缴纳![]() 元的附加费,设月利润为
元的附加费,设月利润为![]() (元)(利润
(元)(利润![]()
![]() 当
当![]() 时,
时,![]() ________元/件,
________元/件,![]() ________元;
________元;
![]() 分别求出
分别求出![]() ,
,![]() 与
与![]() 间的函数关系式(不必写
间的函数关系式(不必写![]() 的取值范围);
的取值范围);
![]() 当
当![]() 为何值时,在甲城市销售的月利润最大?若在乙城市销售月利润的最大值与在甲城市销售月利润的最大值相同,求
为何值时,在甲城市销售的月利润最大?若在乙城市销售月利润的最大值与在甲城市销售月利润的最大值相同,求![]() 的值;
的值;
![]() 如果某月要将
如果某月要将![]() 件产品全部销售完,请你通过分析帮公司决策,选择在甲城市还是在乙城市销售才能使所获月利润较大?
件产品全部销售完,请你通过分析帮公司决策,选择在甲城市还是在乙城市销售才能使所获月利润较大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】许多数学题目都有多种解法,如题目:如图,已知,∠MAN=120°,AC平分∠MAN.∠ABC+∠ADC=180°.求证:AB+AD=AC.

某班第二学习小组经过讨论,提出了三种添加辅助线的方法,请你选择
其中一种方法,完成证明.
方法一:在AN上截取AE=AC,连接CE:
方法二:过点C作CE∥AM交AN于点E
方法三:过点C分别作CE⊥AN于点E,CF⊥AM于点F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1、3,与y轴负半轴交于点C,在下面四个结论中:
①2a+b=0;
②c=﹣3a;
③只有当a=![]() 时,△ABD是等腰直角三角形;
时,△ABD是等腰直角三角形;
④使△ACB为等腰三角形的a的值有三个.
其中正确的结论是_____.(请把正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.

请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AB=BC=5,AC=8,点E、F分别是AC、AB上的动点,将△AEF折叠,使点A落在△ABC的边AC上点A′处(A′不与点A重合),当△A′BC为等腰三角形时,AE的长为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形纸片ABC中,AB=AC,∠BAC=120°,BC=14cm,折叠纸片,使点C和点A重合,折痕与AC,BC交于点D和点E;则折痕DE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青岛某高中允许高三学生从寄宿、走读两种方式中选择一种就读,今年新高三学生总人数与去年相比增加了6%,其中选择寄宿的学生增加了20%,选择走读的学生减少了15%,若去年高三学生的总数为500人,求今年新高三学生选择寄宿和走读的人数分别是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.
(1)BE与DF是否相等?请说明理由;
(2)若AB=14,AD=6,求DF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com