
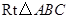 中,
中,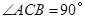 .
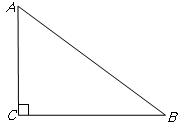
.
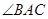 的平分线
的平分线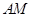 交
交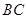 于点
于点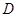 (只保留作图痕迹,不写作法);
(只保留作图痕迹,不写作法);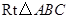 沿某条直线折叠,使点
沿某条直线折叠,使点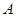 与点
与点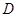 重合,折痕
重合,折痕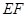 交
交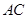 于点
于点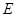 ,交
,交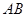 于点
于点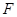 ,连接
,连接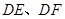 ,再展回到原图形,得到四边形
,再展回到原图形,得到四边形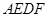 .
.科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
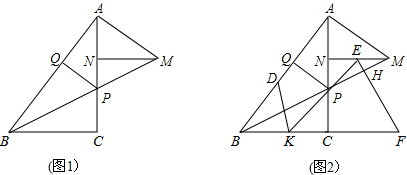
科目:初中数学 来源:不详 题型:解答题
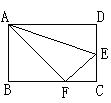
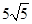 cm,且tan∠EFC=
cm,且tan∠EFC=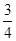 。
。
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
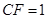 ,则
,则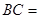 ,△ADE与△ABC的周长之比为 ,△CFG与△BFD的面积之比为 。
,△ADE与△ABC的周长之比为 ,△CFG与△BFD的面积之比为 。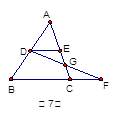
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
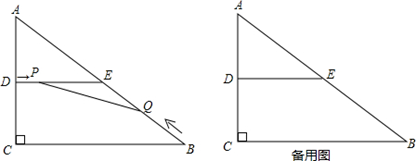
 =1∶29?若存在,求出此时t的值以及点E到PQ的距离h;若不存在,请说明理由.
=1∶29?若存在,求出此时t的值以及点E到PQ的距离h;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com