
| 甲 | 乙 | |
| 价格(万元/台) | 7 | 5 |
| 每台日产量(个) | 100 | 60 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
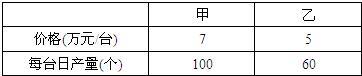 16、某公司为了扩大经营,决定购进6台机器用于生产某种机器零件.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产机器零件的数量如下表所示.经过预算,本次购买机器所用资金不能超过34万元.按该公司要求可以有几种购买方案?
16、某公司为了扩大经营,决定购进6台机器用于生产某种机器零件.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产机器零件的数量如下表所示.经过预算,本次购买机器所用资金不能超过34万元.按该公司要求可以有几种购买方案?查看答案和解析>>
科目:初中数学 来源: 题型:
| 甲 | 乙 | |
| 价格(万元/台) | 5 | 4 |
| 每台日产量(个) | 80 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 机器型号 | 甲 | 乙 |
| 价格(万元/台) | 14 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com