

 ,求OE的长。
,求OE的长。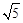
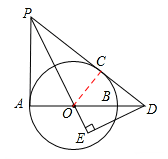
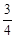 ,∴在Rt△PAD中,AD=8,PD=10。
,∴在Rt△PAD中,AD=8,PD=10。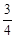 ,∴在Rt△OCD中,OC=OA=3,OD=5。
,∴在Rt△OCD中,OC=OA=3,OD=5。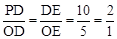 ,即DE=2OE。
,即DE=2OE。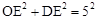 ,即
,即 ,
,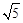 。
。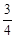 ,可求出CD=4,再证明△OED∽△DEP,根据相似三角形的性质和勾股定理即可求出OE的长。
,可求出CD=4,再证明△OED∽△DEP,根据相似三角形的性质和勾股定理即可求出OE的长。

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源:不详 题型:解答题

 ,求⊙O的直径.
,求⊙O的直径.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

 B.28
B.28 C.29
C.29 D.34
D.34
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
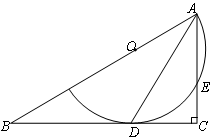
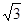 ,求圆弧的半径.
,求圆弧的半径.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
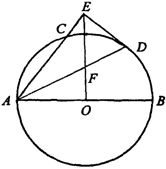
 ,求
,求 的值;
的值;查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ,则图中阴影部分的面积是 。
,则图中阴影部分的面积是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com