练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．化简：（m-n）（m+n）-（m+n）2-mn．

    分析 根据平方差公式以及完全平方公式即可求出答案．

    解答 解：（m-n）（m+n）-（m+n）2-mn
    $\begin{array}{l}={m^2}-{n^2}-（{m^2}+2mn+n{\;}^2）-mn\\={m^2}-{n^2}-{m^2}-2mn-{n^2}-mn\\=-2{n^2}-3mn\end{array}$

    点评 本题考查学生的计算能力，解题的关键是熟练运用乘法公式，本题属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    7．根据图中各点的位置，在数轴上A，B，C，D四个点中，其中表示的数与4-$\sqrt{28}$的结果最接近的点是B．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．关于x的一元二次方程（n+1）x2+x+n2=1的一个根是0，求n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

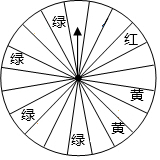    5．某商场为了吸引顾客，设立了一个可以自由转动的转盘（转盘被等分成20个扇形，如图）并规定：顾客在本商场每消费200元，就能获得一次转动转盘的机会，如果转盘停止后，指针正好对准红、黄或绿色区域，顾客就可以分别获得100元、50元、20元的购物券．某顾客消费210元，他转动转盘获得购物券的概率是多少？他得到100元、50元、20元购物券的概率分别是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，四边形ABCD是正方形，AB=4，E是边CD上的点，F是DA延长线上的点、且CE=AF，将△BCE沿BE折叠，得到△BC′E，延长BC′交AD于G．
    （1）求证：△BCE≌△BAF；
    （2）①若DG=1，求FG的长；
    ②若∠CBE=30°，点B和点H关于DF的对称，求证：四边形FHGB是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，点E、F在?ABCD的对角线AC上，且AE=CF．求证：DE=BF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．点P（2a-1，a+2）在x轴上，则点P的坐标为（-5，0）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．先化简，再求值：（$\frac{1}{a-b}$+$\frac{1}{a+b}$）÷$\frac{ab}{{{a^2}-{b^2}}}$+a-10，其中a=8，b=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．（1）计算下列各题
    ①a+2b+3a-2b
    ②2（x2y-3xy2）-3（x2y-4xy2）
    （2）先化简，再求值：
    （2a2-5a）-$\frac{1}{2}$（2a2-4a+2），其中a=$\frac{1}{3}$．

    查看答案和解析>>

    同步练习册答案