
 或
或
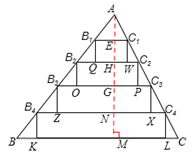
 。
。 。
。 h。∴MN=GN=GH=HE=
h。∴MN=GN=GH=HE=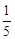 h。
h。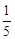 h,时,
h,时,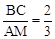 ;
;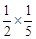 h时,
h时,
 或
或 。
。 ,
, ,求出B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,MN=GN=GH=HE=4,BQ=B2O=B3Z=B4K=4,根据定义判断即可。
,求出B1C1=5,B2C2=10,B3C3=15,B4C4=20,AE=4,AH=8,AG=12,AN=16,MN=GN=GH=HE=4,BQ=B2O=B3Z=B4K=4,根据定义判断即可。 ,求出MN=GN=GH=HE=
,求出MN=GN=GH=HE=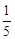 h,分为两种情况:当B3C3=2×
h,分为两种情况:当B3C3=2×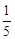 h,时,当B3C3=
h,时,当B3C3=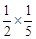 h时,代入求出即可。
h时,代入求出即可。 

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。
,BC=3,△DEF是边长为a(a为小于3的常数)的等边三角形,将△DEF沿AC方向平移,使点D在线段AC上,DE∥AB,设△DEF与△ABC重叠部分的周长为T。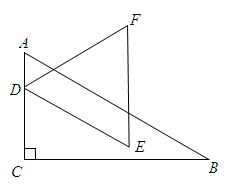
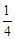 ,当a=2时,求T的值;
,当a=2时,求T的值;查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com