
【题目】已知不等式![]() 的最小整数解为方程
的最小整数解为方程![]() 的解,求代数式
的解,求代数式![]() 的值.
的值.
【答案】-14.
【解析】
试题分析:先求得不等式3(x-2)+5<4(x-1)+6的解集,可求得x的最小整数解是-2,也就是方程2x-ax=3的解是x=-2,把x=-2代入2x-yx=6,求出y=5,代入代数式即可求解.
试题解析:因为3(x-2)+5<4(x-1)+6,
去括号得,3x-6+5<4x-4+6
移项得,3x-4x<-4+6+6-5
合并同类项得,-x<3
系数化为1得,x>-3,
所以x的最小整数解是-2,也就是方程2x-yx=6的解是x=-2,
把x=-2代入2x-yx=6,得到y=5,
代入代数式-9y+6x2+3(y-![]() x2)
x2)
=-6y+4x2
=-6×5+4×4
=-30+16
=-14.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】综合题。
(1)计算:(3﹣π)0﹣ ![]() +|3﹣
+|3﹣ ![]() |+(tan30°)﹣1
|+(tan30°)﹣1
(2)定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算. 比如:2⊕5=2×(2﹣5)+1
=2×(﹣3)+1
=﹣6+1
=﹣5
若3⊕x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2﹣2bx﹣3(b为常数,b<0).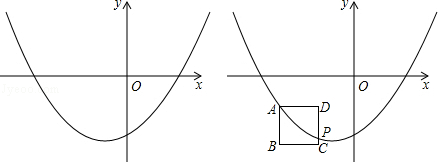
(1)抛物线y=x2﹣2bx﹣3总经过一定点,定点坐标为;
(2)抛物线的对称轴为直线x=(用含b的代数式表示),位于y轴的
侧.
(3)思考:若点P(﹣2,﹣1)在抛物线y=x2﹣2bx﹣3上,抛物线与反比例函数y= ![]() (k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
(k>0,x>0)的图象在第一象限内交点的横坐标为a,且满足2<a<3,试确定k的取值范围.
(4)探究:设点A是抛物线上一点,且点A的横坐标为m,以点A为顶点做边长为1的正方形ABCD,AB⊥x轴,点C在点A的右下方,若抛物线与CD边相交于点P(不与D点重合且不在y轴上),点P的纵坐标为﹣3,求b与m之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,放置的一副三角尺,将含45°角的三角尺斜边中点O为旋转中心,逆时针旋转30°得到如图2,连接OB、OD、AD. 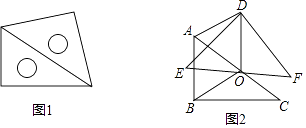
(1)求证:△AOB≌△AOD;
(2)试判定四边形ABOD是什么四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列等式:①由a=b,得5﹣2a=5﹣2b;②由a=b,得ac=bc;③由a=b,得![]() ;④由
;④由![]() ,得3a=2b;
,得3a=2b;
⑤由a2=b2,得a=b.其中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l:y=(x﹣h)2﹣4(h为常数)
(1)如图1,当抛物线l恰好经过点P(1,﹣4)时,l与x轴从左到右的交点为A、B,与y轴交于点C.
①求l的解析式,并写出l的对称轴及顶点坐标.
②在l上是否存在点D,使S△ABD=S△ABC , 若存在,请求出D点坐标,若不存在,请说明理由.
③点M是l上任意一点,过点M做ME垂直y轴于点E,交直线BC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点M的坐标.
(2)设l与双曲线y= ![]() 有个交点横坐标为x0 , 且满足3≤x0≤5,通过l位置随h变化的过程,直接写出h的取值范围.
有个交点横坐标为x0 , 且满足3≤x0≤5,通过l位置随h变化的过程,直接写出h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1 , 得∠A1;∠A1BC和∠A1CD的平分线交于点A2 , 得∠A2;…∠A2016BC和∠A20l6CD的平分线交于点A2017 , 则∠A2017=°. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积为( ) 
A.5
B.10
C.15
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,过点P作PD⊥AB于点D,设运动时间为x(s),△ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是( )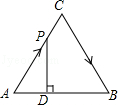
A.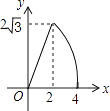
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com