Question

5．在平面直角坐标系中，已知抛物线y=-$\frac{1}{2}$x²+bx+c（b，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，-1），直角顶点B的坐标为（4，-1），三角形另一个顶点C在第一象限．
（1）如图，若该抛物线过A，B两点，求该抛物线的函数表达式；
（2）平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q．
①在滑动过程中，线段PQ的长度是否发生变化，若不变，请直接写出PQ的长度，若改变，请说明理由；
②若点M在直线AC下方，且为平移前（1）中的抛物线上的点，当以M、P、Q三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点M的坐标；
③取BC的中点N，连接NP，BQ．试探究$\frac{PQ}{NP+BQ}$是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．

Answer 1

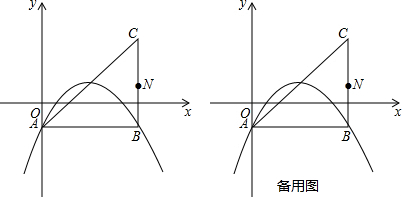
分析 （1）把A、B两点坐标代入抛物线解析式解方程组即可解决问题．
（2）①不变，直线AC与抛物线的交点就是抛物线顶点P，求出PA的长即可解决问题．
②分两种情形：Ⅰ当PQ为直角边时：点M到PQ的距离为2$\sqrt{2}$（即为PQ的长），过点B作直线l₁∥AC，交抛物线y=-$\frac{1}{2}$x²+2x-1于点M，则M为符合条件的点．Ⅱ当PQ为斜边时：MP=MQ=2，可求得点M到PQ的距离为$\sqrt{2}$，如答图1，取AB的中点F，则点F的坐标为（2，-1），过点F作直线l₂∥AC，交抛物线y=-$\frac{1}{2}$x²+2x-1于点M，则M为符合条件的点．
③$\frac{PQ}{NP+BQ}$存在最大值，由①知PQ=2$\sqrt{2}$为定值，则当NP+BQ取最小值时，$\frac{PQ}{NP+BQ}$有最大值，如答图2，取点B关于AC的对称点B′，当B′、Q、F三点共线时，NP+BQ最小，求出这个最小值即可解决问题．

解答 解：（1）由题意，得点B的坐标为（4，-1）．
∵抛物线过A（0，-1），B（4，-1）两点，
∴$\left\{\begin{array}{l}{c=-1}\\{-\frac{1}{2}×16+4b+c=-1}\end{array}\right.$，解得：b=2，c=-1，
∴抛物线的函数表达式为：y=-$\frac{1}{2}$x²+2x-1．               
（2）①不变，PQ=2$\sqrt{2}$．
②∵A（0，-1），C（4，3），
∴直线AC的解析式为：y=x-1，
设平移前抛物线的顶点为P₀，则由（1）可得P₀的坐标为（2，1），且P₀在直线AC上，
∵点P在直线AC上滑动，
∴有平移的性质可得，PQ=2$\sqrt{2}$=AP₀．
若△MPQ为等腰直角三角形，则可分为以下两种情况：
Ⅰ当PQ为直角边时：点M到PQ的距离为2$\sqrt{2}$（即为PQ的长），
由A（0，-1），B（4，-1），P₀（2，1）可知，
△ABP₀为等腰直角三角形，且BP₀⊥AC，BP₀=2$\sqrt{2}$，
如答图1，过点B作直线l₁∥AC，交抛物线y=-$\frac{1}{2}$x²+2x-1于点M，则M为符合条件的点，
∴可设直线l₁的解析式为：y=x+b₁，
∵B（4，-1），∴-1=4+b₁，解得b₁=-5，
∴直线l₁的解析式为：y=x-5，
解方程组$\left\{\begin{array}{l}{y=x-5}\\{y=-\frac{1}{2}{x}^{2}+2x-1}\end{array}\right.$，得：$\left\{\begin{array}{l}{{x}_{1}=4}\\{{y}_{1}=-1}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=-7}\end{array}\right.$，
∴M₁（4，-1），M₂（-2，-7）．
Ⅱ当PQ为斜边时：MP=MQ=2，可求得点M到PQ的距离为$\sqrt{2}$，
如答图1，取AB的中点F，则点F的坐标为（2，-1），
由A（0，-1），F（2，-1），P₀（2，1）可知：
△AFP₀为等腰直角三角形，且点F到直线AC的距离为$\sqrt{2}$，
过点F作直线l₂∥AC，交抛物线y=-$\frac{1}{2}$x²+2x-1于点M，则M为符合条件的点，
∴可设直线l₂的解析式为：y=x+b₂，
∵F（2，-1），∴-1=2+b₂，解得b₁=-3，
∴直线l₂的解析式为：y=x-3，
解方程组$\left\{\begin{array}{l}{y=x-3}\\{y=-\frac{1}{2}{x}^{2}+2x-1}\end{array}\right.$，得：$\left\{\begin{array}{l}{{x}_{1}=1+\sqrt{5}}\\{{y}_{1}=-2+\sqrt{5}}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=1-\sqrt{5}}\\{{y}_{2}=-2-\sqrt{5}}\end{array}\right.$，
∴M₃（1+$\sqrt{5}$，-2+$\sqrt{5}$），M₄（1-$\sqrt{5}$，-2-$\sqrt{5}$）．
综上所述，所有符合条件的点M的坐标为：
M₁（4，-1），M₂（-2，-7），M₃（1+$\sqrt{5}$，-2+$\sqrt{5}$），M₄（1-$\sqrt{5}$，-2-$\sqrt{5}$）．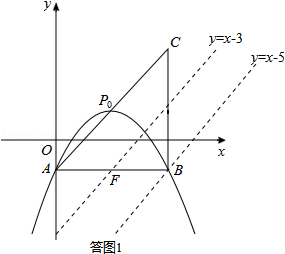

③$\frac{PQ}{NP+BQ}$存在最大值．理由如下：
由①知PQ=2$\sqrt{2}$为定值，则当NP+BQ取最小值时，$\frac{PQ}{NP+BQ}$有最大值．

如答图2，取点B关于AC的对称点B′，易得点B′的坐标为（0，3），BQ=B′Q，
连接QF，FN，QB′，易得FN∥PQ，且FN=PQ，
∴四边形PQFN为平行四边形，
∴NP=FQ，
∴NP+BQ=FQ+B′P≥FB′=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$，
∴当B′、Q、F三点共线时，NP+BQ最小，最小值为2$\sqrt{5}$，
∴$\frac{PQ}{NP+BQ}$的最大值为$\frac{2\sqrt{2}}{2\sqrt{5}}$=$\frac{\sqrt{10}}{5}$．

点评 本题考查二次函数综合题、一次函数、等腰直角三角形的判定和性质、勾股定理、最值问题等知识，解题的关键是把求交点坐标转化为解方程组，构建一次函数是解题的关键，学会把问题转化为我们熟悉的问题，体现了转化的思想，是中考压轴题．