
 如图,PA,PB分别与⊙O相切于点A,B,连接AB,∠APB=60°,AB=5,求PA的长.
如图,PA,PB分别与⊙O相切于点A,B,连接AB,∠APB=60°,AB=5,求PA的长. 科目:初中数学 来源: 题型:选择题
| A. | 6.1×102 | B. | 610×104 | C. | 6.1×105 | D. | 6.1×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
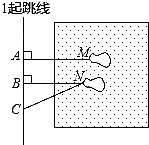 如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )
如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )| A. | 线段AM | B. | 线段BN | C. | 线段CN | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
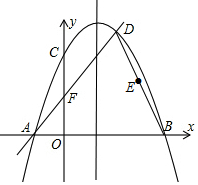 已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).
已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1302×108 | B. | 1.302×103 | C. | 1.302×1010 | D. | 1.302×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
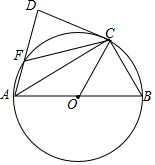 如图,△ABC内接于⊙O,AB是⊙O的直径,DC是⊙O切线,C为切点,AD⊥DC垂足为D,连结AD交⊙O于点F,连接CF.
如图,△ABC内接于⊙O,AB是⊙O的直径,DC是⊙O切线,C为切点,AD⊥DC垂足为D,连结AD交⊙O于点F,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-b | B. | b-a | C. | ab | D. | -ab |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com