


 ,y<0,
,y<0, ×OA•|y|=3
×OA•|y|=3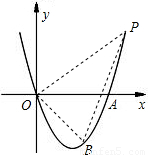
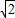 ,OP=4
,OP=4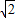 ,
, ×2
×2 ×4
×4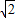 =8.
=8.

科目:初中数学 来源:2007年全国中考数学试题汇编《一次函数》(06)(解析版) 题型:解答题
 x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.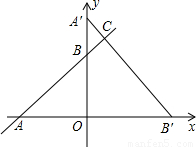
查看答案和解析>>
科目:初中数学 来源:2007年四川省宜宾市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2007年四川省宜宾市中考数学试卷(解析版) 题型:解答题
 x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
x+3的图象与x轴和y轴交于A、B两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《三角形》(16)(解析版) 题型:解答题
 上,OM⊥DE于点M.试求图中阴影部分的面积.(结果保留π)
上,OM⊥DE于点M.试求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com