
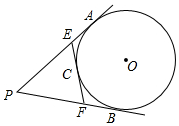
 如图,PA,PB是圆O的切线,切点为分别A,B,圆O的切线EF分别交PA,PB于点E,F,切点C在弧$\widehat{AB}$上,若PA长为2,则△PEF的周长是4.
如图,PA,PB是圆O的切线,切点为分别A,B,圆O的切线EF分别交PA,PB于点E,F,切点C在弧$\widehat{AB}$上,若PA长为2,则△PEF的周长是4. 科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.
如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
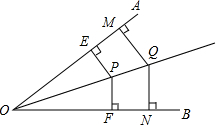 如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.
如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
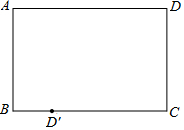 折纸:有一张矩形纸片ABCD(如图所示),要将点D沿某条直线翻折180°,恰好落在BC边上的点D′处,请在图中用尺规作出该直线.(保留作图痕迹)
折纸:有一张矩形纸片ABCD(如图所示),要将点D沿某条直线翻折180°,恰好落在BC边上的点D′处,请在图中用尺规作出该直线.(保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com