
【题目】如图,已知∠AOD=90°,OC平分∠BOD,∠AOB与∠BOC的度数的比是4︰7
(1)求∠AOB的度数.
(2)若以点O为观察中心,以OD为正北方向,则从方位角来说,射线OC在什么方向?

【答案】(1)20°;(2)点O为观察中心,射线OC在北偏东35°
【解析】
(1)设∠AOB=4x°,则∠BOC=7x°,然后由角平分线的定义得到∠BOD=14 x°,根据∠AOD=90°列方程求出x,进而得出∠AOB的度数;
(2)求出∠COD的度数,根据方向角的表示方法,可得答案.
解:(1)设∠AOB=4x°,则∠BOC=7x°
∵OC平分∠BOD
∴∠COD=∠BOC=7x°,∠BOD=14x°
∵∠AOD=90°
∴4x+14x=90
x=5
4x=20
即∠AOB=20°;
(2)∠COD=(5×7)°=35°
∴点O为观察中心,以OD为正北方向,则OA为正东方向,射线OC在北偏东35°.



科目:初中数学 来源: 题型:
【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
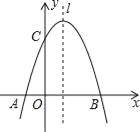
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宿豫区实验初中的图书室平均每天借出图书50册.如果某天借出53册,就记作+3;如果某天借出40册,就记作-10.上星期我校图书室借出图书记录如下:

(1)上星期五借出图书多少册?
(2)上星期二比上星期五多借出图书多少册?
(3)上星期总共借出图书多少册?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的文字,然后按要求解题:
例:1+2+3+ … +100=?
如果一个一个顺次相加显然太繁琐,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法运算律,是可以大大简化计算,提高运算速度的.
因为1+100=2+99=3+98= … =50+51=101
所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解:1+2+3+ … +100
=(1+100)+(2+99)+(3+98)+ … +(50+51)
=101×____________
=____________ .
(1)补全例题的解题过程;
(2)计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商人小周于上周买进某农场品10000![]() ,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000
,每千克2.4元,进入批发市场后共占5个摊位,每个摊位最多能容纳2000![]() 该品种的农产品,每个摊位的市场管理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况.
该品种的农产品,每个摊位的市场管理价为每天20元.下表为本周内该农产品每天的批发价格比前一天的涨跌情况.
星期 | 一 | 二 | 三 | 四 | 五 |
与前一天相比价格的涨跌情况/元 | +0.3 | -0.1 | +0.25 | +0.2 | -0.5 |
当天的交易量/ | 2500 | 2000 | 3000 | 1500 | 1000 |
(1)星期四该农产品的价格为每千克多少元?
(2)本周内该农产品的最高价格为每千克多少元?最低价格为每千克多少元?
(3)小周在销售过程中采用逐步减少摊位个数的方法来降低成本,增加收益,这样他在本周的买卖中共赚了多少钱?请你帮他算一算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用棋子摆成的“上”字:

第一个“上”字 第二个“上”字 第三个“上”字
如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第四、第五个“上”字分别需用 和 枚棋子.
(2)第n个“上”字需用 枚棋子.
(3)如果某一图形共有102枚棋子,你知道它是第几个“上”字吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形AECF中,![]() .CE、CF分别是△ABC的内,外角平分线.
.CE、CF分别是△ABC的内,外角平分线.

(1)求证:四边形AECF是矩形.
(2)当△ABC满足什么条件时,四边形AECF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点M的坐标为(x1,y1),点N的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.
(1)已知点A(2,0),B(0,2![]() ),则以AB为边的“坐标菱形”的最小内角为 ;
),则以AB为边的“坐标菱形”的最小内角为 ;
(2)若点C(1,2),点D在直线y=5上,以CD为边的“坐标菱形”为正方形,求直线CD 表达式;
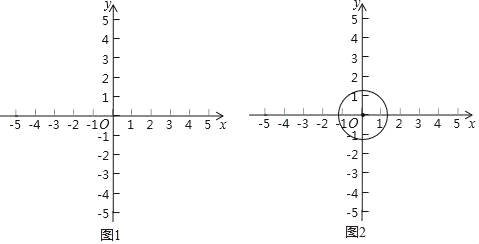
(3)⊙O的半径为![]() ,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com