
 在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为α、b、c,且α=20,∠B=35°,解这个三角形.(精确到0.1,参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为α、b、c,且α=20,∠B=35°,解这个三角形.(精确到0.1,参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)  备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥$\sqrt{2}$ | B. | x≤$\sqrt{2}$ | C. | x<$\sqrt{2}$ | D. | x>$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某“科技创新小组”设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车分别从A、B同时同向出发,沿轨道到达C处停止,甲的速度是乙的速度的2倍,设t(分)后甲、乙两遥控车与B处的距离分别为y1(米)、y2(米),且y1、y2与t的函数关系如图,试根据图象解决下列问题:
某“科技创新小组”设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车分别从A、B同时同向出发,沿轨道到达C处停止,甲的速度是乙的速度的2倍,设t(分)后甲、乙两遥控车与B处的距离分别为y1(米)、y2(米),且y1、y2与t的函数关系如图,试根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
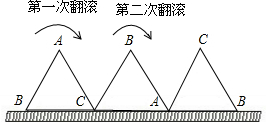 一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π.
一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
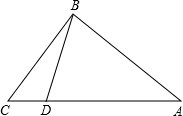 如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,速度为每秒2个单位长度.
如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,速度为每秒2个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
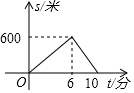 小丽、小亮从学校出发到中心书城购书,小丽步行一段时间后,小亮骑自行车沿相同路线前往,两人均匀前行,他们的路程s(米)与小丽出发时间t(分)之间的函数关系如图,下列说法:①小丽的速度是100米/分;②小丽出发6分钟后小亮才出发;③学校离中心书城的路程为1000米;④小亮骑车的速度是250米/分.其中正确的是( )
小丽、小亮从学校出发到中心书城购书,小丽步行一段时间后,小亮骑自行车沿相同路线前往,两人均匀前行,他们的路程s(米)与小丽出发时间t(分)之间的函数关系如图,下列说法:①小丽的速度是100米/分;②小丽出发6分钟后小亮才出发;③学校离中心书城的路程为1000米;④小亮骑车的速度是250米/分.其中正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y2-49x2 | B. | $\frac{1}{49}-{x^4}$ | C. | -m2-n2 | D. | $\frac{1}{4}{(p+q)^2}-9$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com