
【题目】已知:如图,直线![]() 与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx-3与x轴交于点B(2,0).
与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx-3与x轴交于点B(2,0).
(1)求抛物线的解析式;
(2)点D是抛物线在第三象限图象上的动点,是否存在点D,使得△DAC的面积最大,若存在,请求这个最大值并求出点D的坐标;若不存在,请说明理由;
(3)过点D作DE⊥x轴于E,交AC于F,若AC恰好将△ADE的面积分成1:4两部分,请求出此时点D的坐标.

【答案】(1)![]() ;(2)存在,D
;(2)存在,D![]() ,最大值为
,最大值为![]() ;(3)D
;(3)D![]()
【解析】试题分析:(1)利用一次函数求出点A的坐标,把A、B的坐标代入二次函数解析式即可;(2)设出点D的坐标,再把点F的坐标代入AC求出,△DAC的面积=△DAF的面积+△DFC的面积,即可求出面积的最大值;(3)AC恰好将△ADE的面积分成1:4两部分,所以出现两种情况:DF:EF=1:4, DF:EF=4:1,分类讨论即可.
试题解析:
(1)在![]() 中,当
中,当![]() ,即点A的坐标为
,即点A的坐标为![]()
将A![]() ,B
,B![]() 代入
代入![]() 得
得
![]()
解得![]()
∴抛物线的解析式为: ![]()
(2)设点D的坐标为![]() ,则点F的坐标为
,则点F的坐标为![]()
∴DF= ![]()
∴![]()
![]()
![]()
∵![]() 抛物线开口向下
抛物线开口向下
∴当![]() 时,
时, ![]() 存在最大值
存在最大值![]()
又∵当![]() 时,
时, ![]()
∴存在点D![]() ,使得△ADC的面积最大,最大值为
,使得△ADC的面积最大,最大值为![]()
(3)由题意可得△ADE的面积分成1:4两部分即是点F将DE分成1:4两部分
①当DF:EF=1:4时![]()
解得![]() 或
或![]() (不合题意,舍去)
(不合题意,舍去)
当![]() 时,
时, ![]()
∴点D的坐标为![]()
②当DF:EF=4:1时![]()
解得![]() (不合题意,舍去)或
(不合题意,舍去)或![]() (不合题意,舍去)
(不合题意,舍去)
综上所述存在点D![]() 使得AC恰好将△ADE的面积分成1:4两部分
使得AC恰好将△ADE的面积分成1:4两部分


科目:初中数学 来源: 题型:
【题目】小明早上7点骑自行车从家出发,以每小时12千米的速度到距家4千米的学校上课,行至距学校1千米的地方时,自行车突然发生故障,小明只得改为步行前往学校,如果他想在7点30分之前赶到学校,那么他步行的速度至少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是随机事件的是( )
A.画一个三角形,使其内角和为181°B.明天太阳从西边升起
C.任取一个实数,与其相反数之和为0D.外观相同的10件产品中有两件不合格产品,现从中抽取一件恰为合格品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)用方程解答下列问题
(1)一个角的余角比它的补角的![]() 还少15°,求这个角的度数.
还少15°,求这个角的度数.
(2)几个人共同搬运一批货物,如果每人搬运8箱货物,则剩下7箱货物未搬运;如果每人搬运12箱货物,则缺13箱货物,求参与搬运货物的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某电视塔周围的建筑群平面示意图,这个电视塔的位置用A表示.某人由点B出发到电视塔,他的路径表示错误的是(注:街在前,巷在后)( )
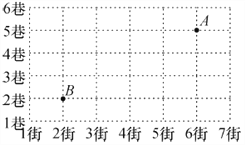
A. (2,2)→(2,5)→(5,6) B. (2,2)→(2,5)→(6,5)
C. (2,2)→(6,2)→(6,5) D. (2,2)→(2,3)→(6,3)→(6,5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com