
【题目】如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.



⑴当x为何值时,△APD是等腰三角形?
⑵若设BE=y,求y关于x的函数关系式;
⑶若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C?若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.
【答案】.
【解析】
⑴解:过D点作DH⊥AB于H,
则四边形DHBC为矩形,
∴DH=BC=4,HB=CD=6 ∴AH=2,AD=2![]() …………………1分
…………………1分
∵AP=x, ∴PH=x-2,
情况①:当AP=AD时,即x=2![]() ……………………………2分
……………………………2分
情况②:当AD=PD时,则AH=PH
∴2=x-2,解得x= 4………………………………………………………·3分
情况③:当AP=PD时,
则Rt△DPH中,x2=42+(x-2)2,解得x=5…………………………………4分
∵2<x<8,∴当x为2![]() 、4、5时,△APD是等腰三角形…………………………5分
、4、5时,△APD是等腰三角形…………………………5分
⑵易证:△DPH∽△PEB ………………………………………………………………7分
∴![]() ,∴
,∴![]() 整理得:y=
整理得:y=![]() (x-2)(8-x)=-
(x-2)(8-x)=-![]() x2+
x2+![]() x-4………8分
x-4………8分
⑶若存在,则此时BE=BC=4,即y=-![]() x2+
x2+![]() x-4=4,整理得:x2-10x+32=0
x-4=4,整理得:x2-10x+32=0
∵△=(-10)2-4×32<0,∴原方程无解,……………………………………………9分
∴不存在点P,使得PQ经过点C……………………………………………………10分
当BC满足0<BC≤3时,存在点P,使得PQ经过点C……………………………12分
1、过D点作DH⊥AB于H,则四边形DHBC为矩形,在Rt△AHD中,由勾股定理可求得DH、AD、PH的值,若△ADP为等腰三角形,则分三种情况:①当AP=AD时,x=AP=AD,②当AD=PD时,有AH=PH,故x=AH+PH,③当AP=PD时,则在Rt△DPH中,由勾股定理可求得DP的值,有x=AP=DP.
2、易证:△DPH∽△PEB![]() ,即
,即![]() ,故可求得y与x的关系式.
,故可求得y与x的关系式.
3、利用△DPH∽△PEB,得出![]() ,进而利用根的判别式和一元二次不等式解集得出即可.
,进而利用根的判别式和一元二次不等式解集得出即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
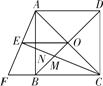
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知EO=![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
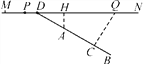
【题目】如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=30°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音(XRS)的影响.
(1)过点A作MN的垂线,垂足为点H,如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排的居民楼,那么此时汽车与点H的距离为多少米?
(2)降低噪音的一种方法是在高架道路旁安装隔音板,当汽车行驶到点Q时,它与这一排居民楼的距离QC为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(精确到1米)(参考数据:![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
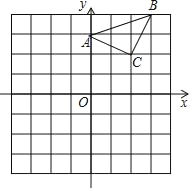
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com