
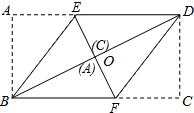
 如图,将矩形纸片ABCD沿BE、DF折叠后,顶点A、C恰好都落在对角线BD的中点O处.若BD=6cm,则四边形BEDF的周长是8$\sqrt{3}$cm.
如图,将矩形纸片ABCD沿BE、DF折叠后,顶点A、C恰好都落在对角线BD的中点O处.若BD=6cm,则四边形BEDF的周长是8$\sqrt{3}$cm. 分析 首先根据折叠可得BO=AB,OD=CD,再根据矩形的性质可得AB=CD=BO=DO,然后在直角三角形ABC中利用勾股定理即可算出CD,BC的长,即可求得结果.
解答 解:根据折叠可得:BO=AB,OD=CD,CF=OF,∠BOF=∠C=90°,
∵四边形ABCD是矩形,
∴AB=CD=BO=DO,
∴CD=$\frac{1}{2}$BD=3,
∵BC2+CD2=BD2,
即32+BC2=62,
解得:BC=3$\sqrt{3}$,
设CF=x,则BF=3$\sqrt{3}$-x,
∴x2+32=${(3\sqrt{3}-x)}^{2}$,
∴x=$\sqrt{3}$,
∴CF=$\sqrt{3}$,BF=2$\sqrt{3}$,
∴DF=$\sqrt{{CF}^{2}{+CD}^{2}}$=2$\sqrt{3}$,
∴四边形BEDF的周长=8$\sqrt{3}$,
故答案为:8$\sqrt{3}$.
点评 此题主要考查了图形的翻折变换,关键是根据翻折方法找出BD=2CD这一条件.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
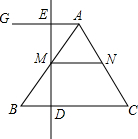 如图,△ABC中,点M是AB边的中点,点D是BC边上一个动点,直线DM交射线AG于点E,AG∥BC.
如图,△ABC中,点M是AB边的中点,点D是BC边上一个动点,直线DM交射线AG于点E,AG∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→“方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第82个点的坐标(10,0).
如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→“方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第82个点的坐标(10,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有“安徽第一楼”之称的安徽省国际金融大厦是具有国际化、专业化、现代化的金融服务场所,它由高度不同的两座楼组成,如图,从左楼丁C处测得右楼楼顶A处的仰角为60°,在左楼楼底D处测得A处的仰角为75°,已知左楼CD高126米,请你利用已知数据估算右楼AB的高.(结果精确到1米,$\sqrt{3}$≈1.7)
有“安徽第一楼”之称的安徽省国际金融大厦是具有国际化、专业化、现代化的金融服务场所,它由高度不同的两座楼组成,如图,从左楼丁C处测得右楼楼顶A处的仰角为60°,在左楼楼底D处测得A处的仰角为75°,已知左楼CD高126米,请你利用已知数据估算右楼AB的高.(结果精确到1米,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | x1 | x2 | x3 | x4 | x5 | x6 | x7 | … |
| y | … | 16 | m | 9 | k | 9 | m | 16 | … |
| A. | ①② | B. | ③④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com