
【题目】已知关于x的一元二次方程x2+2(m+1)x+m21=0.
(1)若方程有两个不相等的实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1,x2,且满足x1+x2+x1x2=5,求实数m的值.
【答案】(1)![]() ;(2)m=4
;(2)m=4
【解析】
(1)当方程有两个不相等的实数根时,△>0,列式计算出m的值;
(2)根据根与系数的关系求出两根的和与两根的积,代入x1+x2+x1x2=5中得:m1=4,m2=-2,再根据△的取值确定其m的值.
(1)△=[2(m+1)]24×1×(m21)>0,
4(m+1)24m2+4>0,
8m>8,
m>1,
则当m>1时,方程有两个不相等的实数根;
(2)x1+x2=2(m+1)=2m2,x1x2=m21,
x1+x2+x1x2=5,
2m2+m21=5,
m22m8=0,
(m4)(m+2)=0,
m1=4,m2=2,
∵方程两实数根分别为x1,x2,
∴△0,
∴m1,
∴m=4.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
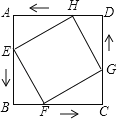
【题目】如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,运动时间t=_____秒时四边形EFGH的面积最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C,点D是该抛物线的顶点,连接AD,BD.

(1)直接写出点C、D的坐标;
(2)求△ABD的面积;
(3)点P是抛物线上的一动点,若△ABP的面积是△ABD面积的![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
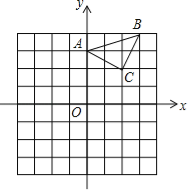
(1)画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标;
(3)作出△ABC关于原点O成中心对称的△A3B3C3,并直接写出B3的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南京某特产专卖店的销售某种特产,其进价为每千克40元,若按每千克60元出售,则平均每天可售出100千克,后来经过市场调查发现,单价每降低3元,平均每天的销售量增加30千克,若专卖店销售这种特产想要平均每天获利2240元,且销量尽可能大,则每千克特产应定价多少元?
(1)方法1:设每千克特产应降价x元,由题意,得方程为:___.
方法2:设每千克特产降价后定价为x元,由题意,得方程为:___.
(2)请你选择一种方法完成解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
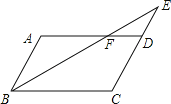
【题目】如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.若△DEF的面积为a,则平行四边形ABCD的面积为 ▲ (用a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC是⊙O的直径,A是⊙O上一点,AD⊥BC,垂足为D,![]() =
=![]() ,BE交AD于点F.
,BE交AD于点F.
(1)∠ACB与∠BAD相等吗?为什么?
(2)判断△FAB的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
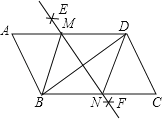
【题目】如图,BD是ABCD的对角线,按以下步骤作图:①分别以点B和点D为圆心,大于![]() BD的长为半径作弧,两弧相交于E,F两点;②作直线EF,分别交AD,BC于点M,N,连接BM,DN.若BD=8,MN=6,则ABCD的边BC上的高为___.
BD的长为半径作弧,两弧相交于E,F两点;②作直线EF,分别交AD,BC于点M,N,连接BM,DN.若BD=8,MN=6,则ABCD的边BC上的高为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场销售某种商品,统计发现:每件盈利![]() 元时,平均每天可销售
元时,平均每天可销售![]() 件.经调查发现,该商品每降价
件.经调查发现,该商品每降价![]() 元,商场平均每天可多售出
元,商场平均每天可多售出![]() 件.
件.
![]() 假如现在库存量太大,部门经理想尽快减少库存,又想销售该商品日盈利达到
假如现在库存量太大,部门经理想尽快减少库存,又想销售该商品日盈利达到![]() 元,请你帮忙思考,该降价多少?
元,请你帮忙思考,该降价多少?
![]() 假如部门经理想销售该商品的日盈利达到最大,请你帮忙思考,又该如何降价?
假如部门经理想销售该商品的日盈利达到最大,请你帮忙思考,又该如何降价?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com