
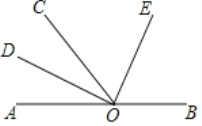
【题目】如图所示,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是 ______ ,∠COD的余角是 ______
(2)OE是∠BOC的平分线吗?请说明理由.
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】我市某化工厂从2008年开始节能减排,控制二氧化硫的排放![]() 图
图![]() ,图
,图![]() 分别是该厂
分别是该厂![]() 年二氧化硫排放量
年二氧化硫排放量![]() 单位:吨
单位:吨![]() 的两幅不完整的统计图,根据图中信息回答下列问题.
的两幅不完整的统计图,根据图中信息回答下列问题.
![]() 该厂
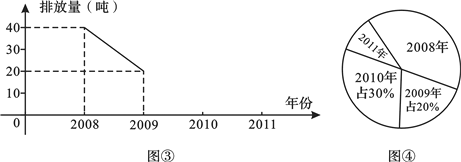
该厂![]() 年二氧化硫排放总量是______ 吨;这四年平均每年二氧化硫排放量是______ 吨
年二氧化硫排放总量是______ 吨;这四年平均每年二氧化硫排放量是______ 吨![]()
![]() 把图中折线图补充完整.
把图中折线图补充完整.
![]() 年二氧化硫的排放量对应扇形的圆心角是______ 度,2011年二氧化硫的排放量占这四年排放总量的百分比是______ .
年二氧化硫的排放量对应扇形的圆心角是______ 度,2011年二氧化硫的排放量占这四年排放总量的百分比是______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,OE. 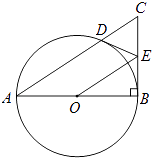
(1)求证:DE是⊙O的切线.
(2)填空: ①当∠CAB=时,四边形AOED是平行四边形;
②连接OD,在①的条件下探索四边形OBED的形状为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)下列图形中,图(a)是正方体木块,把它切去一块,得到如图(b)(c)(d)(e)的木块.
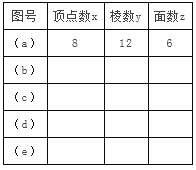
(1)我们知道,图(a)的正方体木块有8个顶点、12条棱、6个面,请你将图(b)、(c)、(d)、(e)中木块的顶点数、棱数、面数填入下表;
(2)上表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数x、棱数y、面数z之间的数量关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E,分别取BC,DE的中点M,N,连接MN.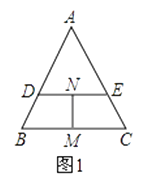
(1)发现:在图1中, ![]() =;
=;
(2)应用:如图2,将△ADE绕点A旋转,请求出 ![]() 的值;
的值;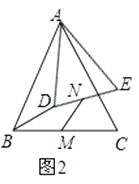
(3)拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DE的中点,若BD⊥CE,请直接写出 ![]() 的值.
的值.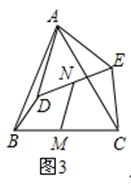
查看答案和解析>>
科目:初中数学 来源: 题型:
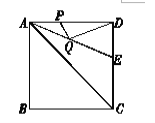
【题目】如图,正方形ABCD的边长是4, ![]() 的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则
的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则![]() 的最小值是( )
的最小值是( )
A. 2 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.求: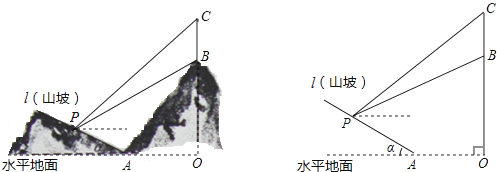
(1)P到OC的距离.
(2)山坡的坡度tanα.
(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的平分线为OM,ON为∠MOA内的一条射线,OG为∠AOB外的一条射线.试说明:
(1)∠MON=![]() (∠BON-∠AON);
(∠BON-∠AON);
(2)∠MOG=![]() (∠AOG+∠BOG).
(∠AOG+∠BOG).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com