
抛物线 与
与 轴交于点A,B,与y轴交于点C,其中点B的坐标为
轴交于点A,B,与y轴交于点C,其中点B的坐标为 .
.
(1)求抛物线对应的函数表达式;]
(2)将(1)中的抛物线沿对称轴向上平移,使其顶点M落在线段BC上,记该抛物线为G,求抛物线G所对应的函数表达式;
(3)将线段BC平移得到线段 (B的对应点为
(B的对应点为 ,C的对应点为
,C的对应点为 ),使其经过(2)中所得抛物线G的顶点M,且与抛物线G另有一个交点N,求点
),使其经过(2)中所得抛物线G的顶点M,且与抛物线G另有一个交点N,求点 到直线
到直线 的距离
的距离 的取值范围.
的取值范围.
(1)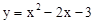 ;(2)
;(2)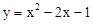 ;(3)
;(3)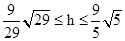 .
.
解析试题分析:(1)根据曲线上点的坐标与方程的关系,将B 代入
代入 求出k即可.
求出k即可.
(2)应用待定系数法求出直线BC的解析式,将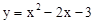 对称轴的
对称轴的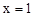 代入BC的解析式求得抛物线G的顶点坐标,从而得到抛物线G所对应的函数表达式.
代入BC的解析式求得抛物线G的顶点坐标,从而得到抛物线G所对应的函数表达式.
(3)连接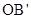 ,过点
,过点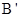 作
作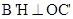 于点H,由
于点H,由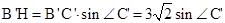 知当
知当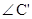 最大时h最大,当
最大时h最大,当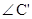 最小时h最小.,即当
最小时h最小.,即当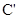 与M重合时,
与M重合时,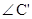 最大,h最大;当
最大,h最大;当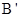 与M重合时,
与M重合时,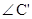 最小,h最小,据此求解即可.
最小,h最小,据此求解即可.
试题解析:(1)将B 代入
代入 得
得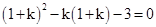 ,解得
,解得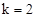 .
.
∴抛物线对应的函数表达式为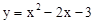 .
.
(2)由题意得,B(3,0),C(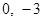 ).
).
∴直线BC的解析式为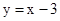 .
.
由(1)得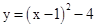 ,
,
∵将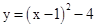 的图象向上平移时,横坐标不变,
的图象向上平移时,横坐标不变,
∴将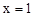 代入
代入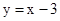 得
得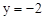 .
.
∴抛物线G的顶点坐标为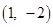 。
。
∴抛物线G所对应的函数表达式为 ,即
,即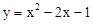 .
.
(3)如图1,连接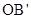 ,过点
,过点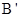 作
作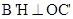 于点H,
于点H,
∵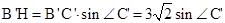 ,
,
∴当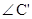 最大时h最大,当
最大时h最大,当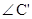 最小时h最小.
最小时h最小.
由图1可知当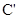 与M重合时,
与M重合时,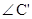 最大,h最大.
最大,h最大.
此时,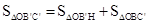 ,即
,即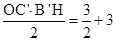 ,∴
,∴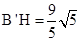 .
.
由图2可知当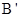 与M重合时,
与M重合时,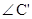 最小,h最小.
最小,h最小.
此时,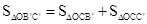 ,即
,即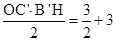 ,
,
此时,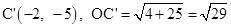 ,∴
,∴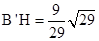 .
.
综上所述,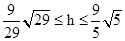 .
.
考点:1.二次函数综合题;2.平移的性质;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.二次函数的性质;6.三角形的面积;7.转换思想的应用.


科目:初中数学 来源: 题型:解答题
如图,经过原点的抛物线y=-x2+bx(b>2)与x轴的另一交点为A,过点P(1, )作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.
)作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.
(1)当b=4时,求点A的坐标及BC的长;
(2)连结CA,求b的适当的值,使得CA⊥CP;
(3)当b=6时,如图2,将△CBP绕着点C按逆时针方向旋转,得到△CB′P′,CP与抛物线对称轴的交点为E,点M为线段B′P′(包含端点)上任意一点,请直接写出线段EM长度的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线y=x2+mx+(m﹣1)与x轴交于点A(x1,0),B(x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.
(1)求抛物线的解析式;
(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线C1:y=(x+m)2(m为常数,m>0),平移抛物线y=﹣x2,使其顶点D在抛物线C1位于y轴右侧的图象上,得到抛物线C2.抛物线C2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,设点D的横坐标为a.
(1)如图1,若m= .
.
①当OC=2时,求抛物线C2的解析式;
②是否存在a,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;
(2)如图2,当OB=2 ﹣m(0<m<
﹣m(0<m< )时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).
)时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.
(1)试用含m的代数式表示A、B两点的坐标;
(2)当点B在原点的右侧,点C在原点的下方时,若 是等腰三角形,求抛物线的解析式;
是等腰三角形,求抛物线的解析式;
(3)已知一次函数 ,点P(n,0)是x轴上一个动点,在(2)的条件下,过点P作垂直于x轴的直线交这个一次函数的图象于点M,交抛物线
,点P(n,0)是x轴上一个动点,在(2)的条件下,过点P作垂直于x轴的直线交这个一次函数的图象于点M,交抛物线 于点N,若只有当
于点N,若只有当 时,点M位于点N的下方,求这个一次函数的解析式.
时,点M位于点N的下方,求这个一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系 中,矩形
中,矩形 的边
的边 在
在 轴上,且
轴上,且 ,
, ,直线
,直线 经过点
经过点 ,交
,交 轴于点
轴于点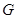 .
.
(1)点 、
、 的坐标分别是
的坐标分别是 ( ),
( ), ( );
( );
(2)求顶点在直线 上且经过点
上且经过点 的抛物线的解析式;
的抛物线的解析式;
(3)将(2)中的抛物线沿直线 向上平移,平移后的抛物线交
向上平移,平移后的抛物线交 轴于点
轴于点 ,顶点为点
,顶点为点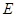 .求出当
.求出当 时抛物线的解析式.
时抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在△ABC中,∠BAC=90°, BC∥x轴,抛物线y=ax2-2ax+3经过△ABC的三个顶点,并且与x轴交于点D、E,点A为抛物线的顶点.
(1)求抛物线的解析式;
(2)连接CD,在抛物线的对称轴上是否存在一点P使△PCD为直角三角形,若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG= DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.
⑴ 求出月销售量y(万件)与销售单价x(元)之间的函数关系式;
⑵ 求出月销售利润z(万元)与销售单价x(元)之间的函数关系式,并在下面坐标系中,画出图象草图;
⑶ 为了使月销售利润不低于480万元,请借助⑵中所画图象进行分析,说明销售单价的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com