【题目】如图□ABCD的对角线AC，BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=600，AB=
BC，连接OE ．下列 结论：①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=
BC 成立的个数有（ ）
A．1个 B．2个 C．3个 D．4个
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案科目：初中数学 来源： 题型：
【题目】已知，点M是二次函数y=ax2（a＞0）图象上的一点，点F的坐标为（0， 
），直角坐标系中的坐标原点O与点M，F在同一个圆上，圆心Q的纵坐标为 
．
（1）求a的值；
（2）当O，Q，M三点在同一条直线上时，求点M和点Q的坐标；
（3）当点M在第一象限时，过点M作MN⊥x轴，垂足为点N，求证：MF=MN+OF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算:
（1）
(2) 
(3) 
(4) 
【答案】(1) 
;(2) 
;(3) 
; (4) 
【解析】试题分析：（1）分子、分母分解因式后约分即可；
（2）先通分计算括号内分式的减法，然后把除法转化为乘法，分子、分母分解因式后约分即可；
（3）第二个分式分子、分母分解因式后约分，然后通分转化为同分母分式，最后依照同分母分式的加减法则计算即可；
（4）先通分计算括号内分式的减法，然后把除法转化为乘法，分子、分母分解因式后约分即可．
试题解析：
解：（1）原式＝
＝
；
（2）原式＝
＝
＝
；
（3）原式＝
＝
＝
＝
＝
；
（4）原式＝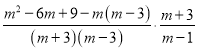
＝
＝
．
点睛：此题考查了分式的混合运算，熟练掌握运算法则和运算顺序是解本题的关键．
【题型】解答题
【结束】
20
【题目】解分式方程：
(1) 
(2) 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解
∵
＜
＜
，即2＜
＜3．
∴
的整数部分为2，小数部分为
﹣2，
∴1＜
﹣1＜2
∴
﹣1的整数部分为1．
∴
﹣1的小数部分为
﹣2
解决问题：已知：a是
﹣3的整数部分，b是
﹣3的小数部分，
求：（1）a，b的值；
（2）（﹣a）3+（b+4）2的平方根．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AM∥BN，∠A=80°，点P是射线AM上动点（与A不重合），BC、BD分别平分∠ABP和∠PBN，交射线AM于C、D．
（1）求∠CBD的度数；
（2）当点P运动时，那么∠APB：∠ADB的度数比值是否随之发生变化？若不变，请求出这个比值；若变化，请找出变化规律；
（3）当点P运动到使∠ACB=∠ABD时，求∠ABC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，BD是△ABC的角平分线，它的垂直平分线分别交AB，BD，BC于点E，F，G，连接ED，DG．
（1）请判断四边形EBGD的形状，并说明理由；
（2）若∠ABC=30°，∠C=45°，ED=2 
，点H是BD上的一个动点，求HG+HC的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（ ）
A. △AFD≌△DCE B. AF=
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某饮料厂以300千克的A种果汁和240千克的B种果汁为原料，配制生产甲、乙两种新型饮料，已知每千克甲种饮料含0.6千克A种果汁，含0.3千克B种果汁；每千克乙种饮料含0.2千克A种果汁，含0.4千克B种果汁．饮料厂计划生产甲、乙两种新型饮料共650千克，设该厂生产甲种饮料x（千克）．
（1）列出满足题意的关于x的不等式组，并求出x的取值范围；
（2）已知该饮料厂的甲种饮料销售价是每1千克3元，乙种饮料销售价是每1千克4元，那么该饮料厂生产甲、乙两种饮料各多少千克，才能使得这批饮料销售总金额最大？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
