解(1)∵二次函数y=x
2+bx+c的顶点M的坐标为(-

,
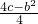
)在直线y=-4x上,
∴
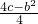
=-

①,
∵图象经过点A(-1,0).
∴0=1-b+c②,
联立①②得

,
解得:
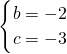
,
故y=x
2-2x-3;
(2)∵y=x
2-2x-3=(x-1)
2-4;
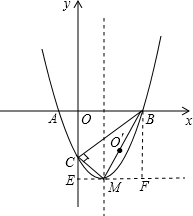
∴与y轴的交点C的坐标是(0,-3),顶点M的坐标是(1,-4)
设y=0,则x
2-2x-3=0,解得x=-1或3,
∴二次函数与x轴的另一个交点B的坐标是(3,0),
过M作ME⊥OE,过B作BF⊥EM交EM于F,
∴OC=3,OB=3,CE=OE-OC=1,MF=2,BF=4,EM=1
在Rt△BOC,Rt△CEM,Rt△BFM中,利用勾股定理得:BC=3

,MC=

,BM=2

,
∵BC
2+MC
2=20,BM
2=2

,
∴BC
2+MC
2=BM
2,
∴△MBC为直角三角形,且∠BCM=90°,

∴⊙O′的直径长为BM=2

;
(3)圆心O′是在直线上,理由如下:
过O′作x轴的垂线,交x轴于R,过O′作y轴的垂线,交y轴于T,交MQ于S,
设⊙O′与x轴的另一个交点为Q,连接MQ,由BM是⊙O′的直径,知∠BQM=90°.
∴Q(1,0),
∵BQ=2,O′R⊥OB,
∴QR=1,
∴OR=2,
在Rt△O′RB中,O′R=

=2,
∴O′的坐标为(2,-2),
∴OT=2,
∵OC=3,
∴TC=1,
∴NC=1,
∴ON=1,
∴N的坐标为(0,-1)
设过PN的直线解析式为y=kx+b,把N的坐标为(0,-1)和P(-2,0)分别代入求得k=-

,b=-1,
∴过PN的直线解析式为y=-

x-1,
∵O′的坐标为(2,-2),
∴-2=-

×2-1=-2,
∴圆心O′是在直线上.
分析:(1)由公式法可表示出二次函数的顶点坐标代入y=-4x,得到关于b,c的关系式,再把A的坐标代入函数解析式又可得到b,c的关系式,联立以上两个关系式解方程组求出b和c的值即可求出这个二次函数的解析式;
(2)分别求出B,C,和M的坐标,利用勾股定理求出BC,MC,BM的长,利用勾股定理的逆定理即可证明三角形为直角三角形,并且BM为圆的直径问题得解;
(3)圆心O′在直线上,过O′作x轴的垂线,交x轴于R,过O′作y轴的垂线,交y轴于T,交MQ于S,利用圆周角定理和勾股定理求出O′,N的坐标,再设经过P(-2,0)、N两点的直线为l的解析式为y=kx+b,把O的坐标代入已求出的一次函数的解析式检验即可.
点评:本题考查了求二次函数和一次函数的解析式、勾股定理的运用、勾股定理的逆定理的运用以及圆周角定理和矩形的性质运用,题目的综合性很强,难度很大.

 已知二次函数y=x2+bx+c的顶点M在直线y=-4x上,并且图象经过点A(-1,0).
已知二次函数y=x2+bx+c的顶点M在直线y=-4x上,并且图象经过点A(-1,0). ,
,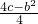 )在直线y=-4x上,
)在直线y=-4x上,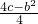 =-
=- ①,
①, ,
,
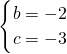 ,
, ,MC=
,MC= ,BM=2
,BM=2 ,
, ,
,
 ;
; =2,
=2, ,b=-1,
,b=-1, x-1,
x-1, ×2-1=-2,
×2-1=-2,

 考前必练系列答案
考前必练系列答案 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( ) 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).