
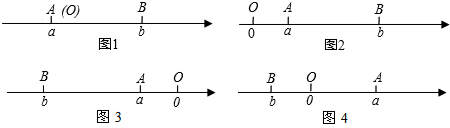
分析 (1)根据材料中的知识可以得到两点之间的距离就是较大的数与较小的数的差,据此即可求解;
(2)根据材料中的知识,即可直接写出结果;
(3)代数式|x-1|+|x+2|表示数轴上一点到1、-2两点的距离的和,根据两点之间线段最短,进而得出答案.
解答 解:(1)数轴上表示2和5的两点之间的距离是:5-2=3;
数轴上表示-2和-5的两点之间的距离是-2-(-5)=3,
数轴上表示1和-3的两点之间的距离是1-(-3)=4;
故答案为:3;3;4;
(2)数轴上表示x和-1的两点之间的距离是|x+1|,
|AB|=2,则|x+1|=2,故x=1或-3;
故答案为:|x+1|,1或-3;
(3)若|x+1|+|x-2|取最小值,那么表示x的点M在-1和2之间的线段上,
所以-1≤x≤2;
故答案为:-1≤x≤2.
点评 此题主要考查了绝对值、数轴等知识,用几何方法借助数轴来求解,非常直观,体现了数形结合的优点.


科目:初中数学 来源: 题型:选择题
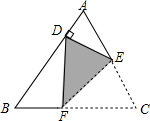 如图,将等边△ABC折叠,使得点C落在AB边上的点D处,若∠ADE=90°,AD=2,则AC的长为( )
如图,将等边△ABC折叠,使得点C落在AB边上的点D处,若∠ADE=90°,AD=2,则AC的长为( )| A. | 4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com