
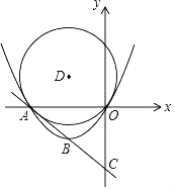
【题目】 已知:直线y=-x-4分别交x、y轴于A、C两点,点B为线段AC的中点,抛物线y=ax2+bx经过A、B两点,
(1)求该抛物线的函数关系式;
(2)以点B关于x轴的对称点D为圆心,以OD为半径作⊙D,连结AD、CD,问在抛物线上是否存在点P,使S△ACP=2S△ACD?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,若E为⊙D上一动点(不与A、O重合),连结AE、OE,问在x轴上是否存在点Q,使∠ACQ:∠AEO=2:3?若存在,请求出所有满足条件的点Q的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2+2x;(2)P坐标为(-3-
x2+2x;(2)P坐标为(-3-![]() ,7+
,7+![]() )或(-3+
)或(-3+![]() ,7-
,7-![]() );(3)Q坐标为(4
);(3)Q坐标为(4![]() -8,0)、(-4
-8,0)、(-4![]() -8,0)、(4,0).
-8,0)、(4,0).
【解析】
(1)求直线y=-x-4与坐标轴交点A、C坐标,求AC中点B坐标,即能用待定系数法求抛物线的函数关系式;
(2)根据点B坐标(-2,-2),可得D坐标为(-2,2),所以△ADO、△ACO均为等腰直角三角形,连接AD并延长交y轴于点F,可知使S△ACP=2S△ACD的点P在过点F且平行于直线y=-x-4的直线上,求出直线与抛物线交点即使所求点P;
(3)由(2)可知,∠AEO度数有两种情况,当点E在优弧AO上时,∠ACQ=![]() ∠AEO=30°.构造直角三角形列方程即可求出Q坐标,当点E在劣弧AO上时,∠AEO=135°,∠ACQ=90°.由等腰直角三角形性质和对称即可求出点Q.
∠AEO=30°.构造直角三角形列方程即可求出Q坐标,当点E在劣弧AO上时,∠AEO=135°,∠ACQ=90°.由等腰直角三角形性质和对称即可求出点Q.
解:(1)∵直线y=-x-4中,y=0时,x=-4;x=0时,y=-4,
∴A(-4,0),C(0,-4),
∵点B为AC中点,
∴B(-2,-2),
∵抛物线y=ax2+bx经过A、B两点,
∴![]() ,
,
解得:![]() ,
,
∴抛物线的函数关系式为y=![]() x2+2x.
x2+2x.
(2)在抛物线上存在点P使S△ACP=2S△ACD.
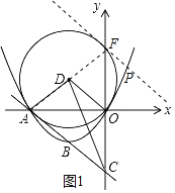
如图1,连接AD并延长交y轴于点F,
∵y=![]() x2+2x=
x2+2x=![]() (x-2)2-2,
(x-2)2-2,
∴点B为抛物线的顶点,
∵点D为点B关于x轴的对称点,
∴D(-2,2)在抛物线的对称轴上,
∴DA=DO,∠DAO=∠DOA=45°,
∵OA=OC=4,∠AOC=90°,
∴∠OAC=45°,
∴∠DAC=∠DAO+∠OAC=90°,
∴S△ACD=![]() ACAD,
ACAD,
∵∠AOF=90°,
∴AF为⊙D
∴AF=2AD,OF=OA=4即F(0,4),
∵S△ACP=2S△ACD=2![]() ACAD=
ACAD=![]() AC2AD=
AC2AD=![]() ACAF,
ACAF,
∴点P在过点F且平行于直线y=-x-4的直线上,
∴直线PF解析式为y=-x+4,
∵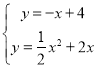 ,
,
解得: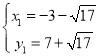 ;
;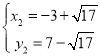 .
.
∴点P坐标为(-3-![]() ,7+
,7+![]() )或(-3+
)或(-3+![]() ,7-
,7-![]() );
);
(3)在x轴上存在点Q使∠ACQ:∠AEO=2:3.
∵∠OAD=∠ODA=45°,
∴∠ADO=90°,
∵点E在⊙D上且不与A、O重合,∠ACQ:∠AEO=2:3.
①如图2,当点E在优弧AO上时,∠AEO=![]() ∠ADO=45°,
∠ADO=45°,
∴∠ACQ=![]() ∠AEO=30°,
∠AEO=30°,
过点Q作QG垂直直线AC于点G,设QG=t,
∴Rt△CQG中,CQ=2QG=2t,CG=![]() QG=
QG=![]() t.
t.
∴∠GAQ=∠OAC=45°,
∴Rt△AGQ中,AG=QG=t,AQ=![]() QG=
QG=![]() t.
t.
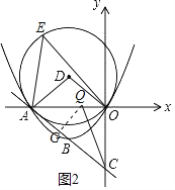
i)若点Q在线段AO上时,如图2:
则AC=AG+CG=t+![]() t=4
t=4![]() ,
,
解得:t=2![]() -2
-2![]() ,
,
∴AQ=![]() ,
,
∴xQ=-4+4![]() -4=4
-4=4![]() -8;
-8;
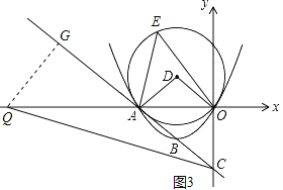
ii)若点Q在线段OA延长上时,如图3:
则AC=CG-AG=![]() t-t=4
t-t=4![]() ,
,
解得:![]() ,
,
∴AQ=![]() ,
,
∴xQ=-4-(4![]() +4)=-4
+4)=-4![]() -8,
-8,
②当点E在劣弧AO上时,∠AEO=![]() (360°-∠ADO)=135°,
(360°-∠ADO)=135°,
∴∠ACQ=![]() ∠AEO=90°.
∠AEO=90°.
∵∠CAO=45°,△ACO是等腰直角三角形,
∴Q点与A点对称,A (-4,0)
∴xQ=4.
综上所述:满足条件的点Q有三个,坐标分别为(4![]() -8,0)、(-4
-8,0)、(-4![]() -8,0)、(4,0)
-8,0)、(4,0)


科目:初中数学 来源: 题型:
【题目】新华商场为迎接家电下乡活动销售某种冰箱,每台进价为2500元,市场调研表明;当销售价定为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
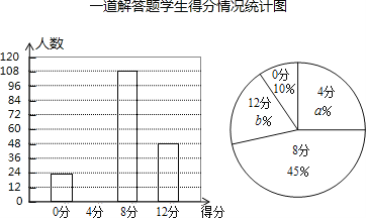
【题目】有一道满分12分的解答题,按评分标准,所有考生的得分只有四种:0分,4分,8分,12分.老师为了了解学生的得分情况与题目的难易情况,从所有考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a=______,b=______,并把条形统计图补全;
(2)已知难度系数的计算公式为![]() ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0≤L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L≤1时,此题为容易题.试问此题对于这些考生来说属于哪一类?请说明理由.
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0≤L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L≤1时,此题为容易题.试问此题对于这些考生来说属于哪一类?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
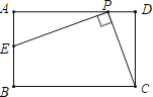
【题目】 如图,在矩形ABCD中,AB=6,BC=10,P是AD边上一动点(不含端点A,D),连接PC,E是AB边上一点,设BE=a,若存在唯一点P,使∠EPC=90°,则a的值是( )
A.![]() B.
B.![]() C.3D.6
C.3D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从-3、-1、![]() 、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=-x+a的图象与坐标轴围成三角形的面积不超过4的概率为______.
、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=-x+a的图象与坐标轴围成三角形的面积不超过4的概率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在![]() 地时距地面的高度
地时距地面的高度![]() 为 米;
为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件,经调查发现,这种商品的销售单价每提高1元,其销售量相应减少10件.
(1)求销售量![]() 件与销售单价
件与销售单价![]() 元之间的关系式;
元之间的关系式;
(2)当销售单价![]() 定为多少,才能使每天所获销售利润最大?最大利润是多少?
定为多少,才能使每天所获销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
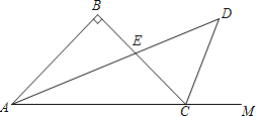
【题目】如图,在△ABC中,∠B=90°,AB=BC,∠BCM是△ABC的外角,∠BAC、∠BCM的平分线交于点D,AD与BC交于点E,若BE=2,则AEDE=____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com