
分析 (1)根据计算器的使用:shift→sin→函数值→=,可得答案;
(2)根据计算器的使用:shift→cos→函数值→=,可得答案;
(3)根据计算器的使用:shift→tan→函数值→=,可得答案.
解答 解:(1)sinA=0.6374,则∠A=39°35′24″;sinB=0.0438,则∠B=2°30′36″;
(2)cosA=0.6241,则∠A=51°22′48″;cosB=0.1742,则∠B=79°57′36″;
(3)tanA=4.8525,则∠A=78°21′0″;tanB=0.8234,则∠B=39°27′36″;
故答案为:39°35′24″;2°30′36″;51°22′48″;79°57′36″;78°21′0″;39°27′36″.
点评 本题考查了计算器,正确使用计算器:shift→sin→函数值→=是解题关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
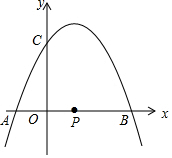 如图,在直角坐标系中,A(-1,0),B(3,0),以A、B为直径的圆⊙P交y轴的正半轴于点C,抛物线y=ax2+bx+c经过点A、B、C.
如图,在直角坐标系中,A(-1,0),B(3,0),以A、B为直径的圆⊙P交y轴的正半轴于点C,抛物线y=ax2+bx+c经过点A、B、C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
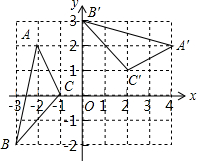 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )| A. | ( 0,1) | B. | ( 1,-1) | C. | ( 0,-1) | D. | ( 1,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com