
 在平面直角坐标系xOy中,△ABC的位置如图所示.
在平面直角坐标系xOy中,△ABC的位置如图所示.分析 (1)根据平面直角坐标系可得△ABC各个顶点的坐标;
(2)首先利用勾股定理计算出AB、AC、BC长,再利用勾股定理逆定理可证出△ABC为等腰直角三角形;
(3)首先确定A、B、C三点关于y轴对称的对称点位置,然后再连接即可.
解答 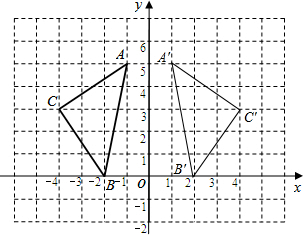 解:(1)A(-1,5),B(-2,0),C(-4,3).
解:(1)A(-1,5),B(-2,0),C(-4,3).
(2)△ABC为等腰直角三角形.
理由如下:由勾股定理有:$AB=\sqrt{26}$,$AC=\sqrt{13}$,$BC=\sqrt{13}$
∴AC=BC,AC2+BC2=AB2
∴△ABC为等腰直角三角形.
(3)如图所示.
点评 此题主要考查了作图--轴对称变换,以及勾股定理和勾股定理逆定理,关键是掌握在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方;如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | -2xy | B. | 6xy | C. | -6xy | D. | 2xy |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,分别以AB,AC为边在△ABC外作等边三角形△ABE和△ACD.已知∠ABC=30°,AB=3,BC=4.则BD的长为5.
如图,在△ABC中,分别以AB,AC为边在△ABC外作等边三角形△ABE和△ACD.已知∠ABC=30°,AB=3,BC=4.则BD的长为5.查看答案和解析>>
科目:初中数学 来源:2017届广东省广州市九年级下学期3月月考数学试卷(解析版) 题型:判断题
如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.
(1)求抛物线的解析式;
(2)猜想并探究:对于任意一点P,PD与PF的差是否为固定值,如果是,请求出此定值,如果不是,请说明理由;
(3)求:①当△PDE的周长最小时的点P坐标;②使△PDE的面积为整数的点P的个数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com