
【题目】如图,点![]() ,过点
,过点![]() 做直线
做直线![]() 平行于
平行于![]() 轴,点
轴,点![]() 关于直线
关于直线![]() 对称点为
对称点为![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)点![]() 在直线
在直线![]() 上,且位于
上,且位于![]() 轴的上方,将
轴的上方,将![]() 沿直线
沿直线![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 恰好落在直线
恰好落在直线![]() 上,求点
上,求点![]() 的坐标和直线
的坐标和直线![]() 的解析式;
的解析式;
(3)设点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,当
上,当![]() 为等边三角形时,求点
为等边三角形时,求点![]() 的坐标.
的坐标.
【答案】(1)(3,0);(2)A(1,![]() );直线BD为
);直线BD为![]() ;(3)点P的坐标为(
;(3)点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)根据题意,点B、C关于点M对称,即可求出点C的坐标;
(2)由折叠的性质,得AB=CB,BD=AD,根据勾股定理先求出AM的长度,设点D为(1,a),利用勾股定理构造方程,即可求出点D坐标,然后利用待定系数法求直线BD.
(3)分两种情形:如图2中,当点P在第一象限时,连接BQ,PA.证明点P在AC的垂直平分线上,构建方程组求出交点坐标即可.如图3中,当点P在第三象限时,同法可得△CAQ≌△CBP,可得∠CAQ=∠CBP=30°,构建方程组解决问题即可.
解:(1)根据题意,
∵点B、C关于点M对称,且点B、M、C都在x轴上,
又点B(![]() ),点M(1,0),
),点M(1,0),
∴点C为(3,0);
(2)如图:

由折叠的性质,得:AB=CB=4,AD=CD=BD,
∵BM=2,∠AMB=90°,
∴![]() ,
,
∴点A的坐标为:(1,![]() );
);
设点D为(1,a),则DM=a,BD=AD=![]() ,
,
在Rt△BDM中,由勾股定理,得
![]() ,
,
解得:![]() ,
,
∴点D的坐标为:(1,![]() );
);
设直线BD为![]() ,则
,则
 ,解得:
,解得: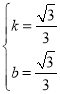 ,
,
∴直线BD为:![]() ;
;
(3)如图2中,当点P在第一象限时,连接BQ,PA.
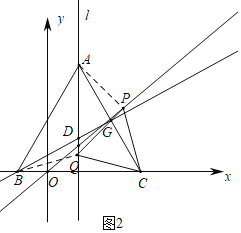
∵△ABC,△CPQ都是等边三角形,
∴∠ACB=∠PCQ=60°,
∴∠ACP=∠BCQ,
∵CA=CB,CP=CQ,
∴△ACP≌△BCQ(SAS),
∴AP=BQ,
∵AD垂直平分线段BC,
∴QC=QB,
∴PA=PC,
∴点P在AC的垂直平分线上,
由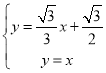 ,解得
,解得 ,
,
∴P(![]() ,
,![]() ).
).
如图3中,当点P在第三象限时,同法可得△CAQ≌△CBP,
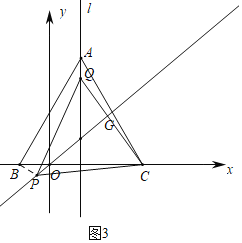
∴∠CAQ=∠CBP=30°,
∵B(-1,0),
∴直线PB的解析式为![]() ,
,
由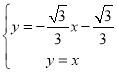 ,解得:
,解得: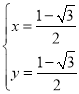 ,
,
∴P(![]() ,
,![]() ).
).


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】春节期间,小丽一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
租车公司:按日收取固定租金80元,另外再按租车时间计费.
共享汽车:无固定租金,直接以租车时间(时)计费.
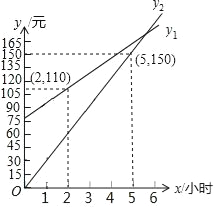
如图是两种租车方式所需费用y1(元)、y2(元)与租车时间x(时)之间的函数图象,根据以上信息,回答下列问题:
(1)分别求出y1、y2与x的函数表达式;
(2)请你帮助小丽一家选择合算的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,BC=10,AC⊥AB,点E、F分别是BC,AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形时,请求出AE的长度;
(3)若四边形AECF是矩形时,请直接写出BE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】曹州牡丹园售票处规定:入园门票每张80元.非节假日的票价打6折售票;节假日根据团队人数实行分段售票:不超过10人,则按原票价购买;超过10人,则其中10人按原票价购买,超过部分的按原票价打8折购买.某旅行社带团x人到牡丹园游览,设非节假日的购票款为y1元,在节假日的购票款为y2元.求:
(1)当x>10时,y1、y2与x的函数关系式;
(2)该旅行社在今年5月1日带甲团与5月10日(非节假日)带乙团到牡丹园游览,甲、乙两个团各25人,请问乙团比甲团便宜多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
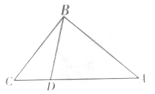
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上的动点,点
边上的动点,点![]() 从点
从点![]() 出发,沿边
出发,沿边![]() 向点
向点![]() 运动,当运动到点
运动,当运动到点![]() 时停止,若设点
时停止,若设点![]() 运动的时间为
运动的时间为![]() 秒,点
秒,点![]() 运动的速度为每秒2个单位长度.
运动的速度为每秒2个单位长度.

(1)当![]() 时,
时,![]() = ,
= ,![]() = ;
= ;
(2)求当![]() 为何值时,
为何值时,![]() 是直角三角形,说明理由;
是直角三角形,说明理由;
(3)求当![]() 为何值时,
为何值时,![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
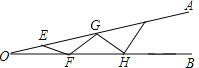
【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH,添的钢管长度都与OE相等,则最多能添加这样的钢管_____根.
查看答案和解析>>
科目:初中数学 来源: 题型:
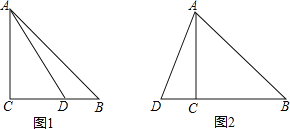
【题目】在△ABC中,∠C=90°,AC=BC,点D在射线BC上(不与点B、C重合),连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE.
(1)如图1,点D在BC边上.
①依题意补全图1;
②作DF⊥BC交AB于点F,若AC=8,DF=3,求BE的长;
(2)如图2,点D在BC边的延长线上,用等式表示线段AB、BD、BE之间的数量关系(直接写出结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
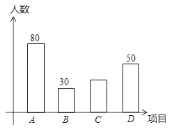
【题目】某中学开展“阳光体育一小时”活动.根据学校事假情况,决定开设四项运动项目:A:踢毽子;B:篮球;C:跳绳;D:乒乓球.为了解学生最喜欢哪一种运动项目,随机抽取了n名学生进行问卷调查,每位学生在问卷调查时都按要求只选择了其中一种喜欢的运动项目.收回全部问卷后,将收集到的数据整理并绘制成如下的统计图,若参与调查的学生中喜欢A方式的学生的人数占参与调查学生人数的40%.根据统计图提供的信息,解答下列问题:
(1)求n的值.
(2)求参与调查的学生中喜欢C的学生的人数.
(3)根据统计结果,估计该校1800名学生中喜欢C方式的学生比喜欢B方式的学生多的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
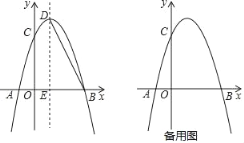
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(3)若点P是x轴上方抛物线上的动点,以PB为边作正方形PBFG,随着点P的运动,正方形的大小、位置也随着改变,当顶点F或G恰好落在y轴上时,请直接写出点P的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com