
【题目】如图,小明将一张正方形卡纸剪去一个宽为4cm的长方形(记作A)后,再将剩下的长方形卡纸剪去一个宽为5cm的长方形(记作B).

(1)若长方形A与B的面积均为Scm2,求S的值.
(2)若A的周长是B的周长的![]() 倍,求原正方形的边长.
倍,求原正方形的边长.
【答案】(1)S=80cm2;(2)原正方形的边长为17cm.
【解析】
(1)根据正方形的边长相等,利用长方形面积公式列方程求出S的值即可;
(2)设原来正方形纸的边长是xcm,则第一次剪下的长条的长是xcm,宽是4cm,第二次剪下的长条的长是x-4cm,宽是5cm,利用长方形周长公式列方程求出x的值即可.
(1)∵长方形A与B的面积均为Scm2,正方形的边长相等,
∴![]() ,
,
解得:S=80,
(2)设原来正方形纸的边长是xcm,
∴第一次剪下的长条的长是xcm,宽是4cm,第二次剪下的长条的长是x-4cm,宽是5cm,
∵A的周长是B的周长的![]() 倍,
倍,
∴2(x+4)=![]() ×2(x-4+5),
×2(x-4+5),
解得:x=17.
∴原正方形的边长为17cm.


科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,∠AOC=30°,点C在AB的上方.MON为直角三角板,O为直角顶点,![]() ,ON在射线OC上.将三角板MON绕点O以每秒6°的速度沿逆时针方向旋转,与此同时,射线OC绕点O以每秒11°的速度沿逆时针方向旋转,当射线OC与射线OA重合时,所有运动都停止.设运动的时间为t秒,
,ON在射线OC上.将三角板MON绕点O以每秒6°的速度沿逆时针方向旋转,与此同时,射线OC绕点O以每秒11°的速度沿逆时针方向旋转,当射线OC与射线OA重合时,所有运动都停止.设运动的时间为t秒,
(1)旋转开始前,∠MOC= °,∠BOM= °;
(2)运动t秒时,OM转动了 °,t为 秒时,OC与OM重合;
(3)t为何值时,∠MOC=35°?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.
(1)求证:点P为![]() 的中点;
的中点;
(2)若∠C=∠D,求四边形BCPD的面积.
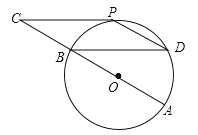
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,将一块含有30°角的直角三角尺DEF按如图所示放置,让三角尺在BC所在的直线上向右平移.如图①,当点E与点B重合时,点A恰好落在三角尺的斜边DF上.
(1)利用图①证明:EF=2BC.
(2)在三角尺的平移过程中,在图②中线段AH=BE是否始终成立(假定AB,AC与三角尺的斜边的交点分别为G,H)?如果成立,请证明;如果不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为![]() .
.
(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,①检测深圳的空气质量; ②为了解某中东呼吸综合征(MERS)确诊病人同一架飞机乘客的健康情况;③为保证“神舟9号”成功发射,对其零部件进行检查;④调查某班50名同学的视力情况。其中适合采用抽样调查的是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com