
已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB,AC相交于D点,双曲线y= (x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①菱形OABC的面积为80; ②E点的坐标是(4,8);③双曲线的解析式为y=
(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①菱形OABC的面积为80; ②E点的坐标是(4,8);③双曲线的解析式为y= (x>0); ④
(x>0); ④ ,其中正确的结论有( )个。
,其中正确的结论有( )个。
| A.1 | B.2 | C.3 | D.4 |
C.
解析试题分析:过点C作CF⊥x轴于点F,由OB•AC=160可求出菱形的面积,由A点的坐标为(10,0)可求出CF的长,由勾股定理可求出OF的长,故可得出C点坐标,对角线OB、AC相交于D点可求出D点坐标,用待定系数法可求出双曲线y= (x>0)的解析式,由反比例函数的解析式与直线BC的解析式联立即可求出E点坐标;由sin∠COA=
(x>0)的解析式,由反比例函数的解析式与直线BC的解析式联立即可求出E点坐标;由sin∠COA= 可求出∠COA的正弦值;根据A、C两点的坐标可求出AC的长,由OB•AC=160即可求出OB的长.
可求出∠COA的正弦值;根据A、C两点的坐标可求出AC的长,由OB•AC=160即可求出OB的长.
过点C作CF⊥x轴于点F,
∵OB•AC=160,A点的坐标为(10,0),
∴ ,菱形OABC的面积为80,故①正确;
,菱形OABC的面积为80,故①正确;
又菱形OABC的边长为10,
∴CF=
在Rt△OCF中,
∵OC=10,CF=8,
∴ ,
,
∴C(6,8),
∵点D时线段AC的中点,
∴D点坐标为( ,
, ),即(8,4),
),即(8,4),
∵双曲线y= (x>0)经过D点,
(x>0)经过D点,
∴4= ,即k=32,
,即k=32,
∴双曲线的解析式为:y= (x>0),故③错误;
(x>0),故③错误;
∵CF=8,
∴直线CB的解析式为y=8,
∴ ,解得x=4,y=8,
,解得x=4,y=8,
∴E点坐标为(4,8),故②正确;
∵CF=8,OC=10,
∴ ,故④正确;
,故④正确;
故选C.
考点: 反比例函数.


科目:初中数学 来源: 题型:单选题
如图,A、B、C是反比例函数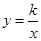 (k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
(k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
A.4条 B.3条 C.2条 D.1条
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,已知A、B是反比例函数 上的两点,BC∥x轴,交y轴于C,动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过运动路线上任意一点P作PM⊥x轴于M,PN⊥y轴于N,设四边形OMPN的面积为S,P点运动的时间为t,则S关于t的函数图象大致是( )
上的两点,BC∥x轴,交y轴于C,动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过运动路线上任意一点P作PM⊥x轴于M,PN⊥y轴于N,设四边形OMPN的面积为S,P点运动的时间为t,则S关于t的函数图象大致是( )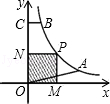
A B
B C
C D
D
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数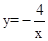 和
和 的图象交于点A和点B.若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为 ( )
的图象交于点A和点B.若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为 ( )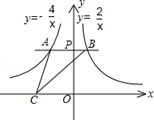
A.3 B.4 C.5 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com