
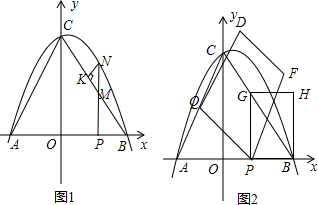
���� ��1����y=0���ⷽ��-$\frac{1}{3}$x2+$\frac{1}{3}x$+4=0�������A��B���꣬�����ô���ϵ�������ֱ��BC��
��2����ͼ1�У���P��a��0����ֻҪ֤��MN=PB���г����̼��ɽ�����⣮
��3������ͼ2�У�����Գ�ͼ��Ϊ����ʱ���г���������˶�ʱ�伴�ɣ�����ͼ3�У�����Գ�ͼ����������ʱ���г��������ʱ�伴�ɣ�
��� �⣺��1����y=0����-$\frac{1}{3}$x2+$\frac{1}{3}x$+4=0�����x=4��-3��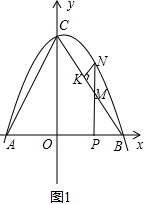
���A���꣨-3��0������B���꣨4��0����
��ֱ��BC����ʽΪy=kx+b����B��4��0����C��0��4������
��$\left\{\begin{array}{l}{b=4}\\{4k+b+0}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$��
��ֱ��BC����ʽΪy=-x+4��
��2����ͼ1�У���PN��OC��NK��BC��
���MPB=��MKN=90�㣬
�ߡ�PMB=��NMK��
���MNK�ס�MPB��
�ߡ�MNK���MPB�������Ϊ1��2��
��BM=$\sqrt{2}$MN��
��OB=OC��
���PBM=45�㣬
��BM=$\sqrt{2}$PB��
��MN=PB����P��a��0������MN=-$\frac{1}{3}$a2+$\frac{1}{3}$a+4+a-4=-$\frac{1}{3}$a2+$\frac{4}{3}$a��BP=4-a��
��-$\frac{1}{3}$a2+$\frac{4}{3}$a=4-a��
���a=3��4����������
��PB=1��t=$\frac{1}{5}$��
��3����ͼ2�У�����Գ�ͼ��Ϊ����ʱ��PF=PG��GM=FM��
��BP=PG=AQ��PQ=PF��
��AQ=PQ=5t��
����Q��QN��AP����AN=NP���ɡ�AQN�ס�ACQ��
��$\frac{AQ}{AC}$=$\frac{AN}{AO}$��
��$\frac{5t}{5}$=$\frac{AN}{3}$��
��AN=3t��
��AP=2AN=6t��
��AP+BP=AB��
��5t+6t=7��
��t=$\frac{7}{11}$��
��PB=PF=$\frac{35}{11}$��
�ɡ�ACO�ס�FPR�ס�MFT��
��$\frac{FP}{FR}$=$\frac{AC}{AO}$��
��FR=$\frac{21}{11}$��TF=$\frac{14}{11}$��
��$\frac{FM}{TF}$=$\frac{AC}{AO}$��
��FM=$\frac{35}{22}$��
��S=2��$\frac{1}{2}$��PF��FM=$\frac{1225}{242}$��
����ͼ3�У�����Գ�ͼ����������ʱ��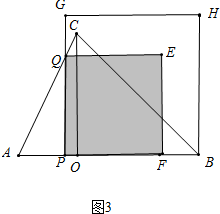
3t+5t=7��
��t=$\frac{7}{8}$��
��S=$\frac{49}{4}$��
���� ���⿼����κ����ۺ��⡢����ϵ���������������ε��ж������ʵ�֪ʶ������Ĺؼ����������մ���ϵ�������к�������ʽ��ѧ���÷��̵�˼��˼�����⣬��Ҫ��ȷ����ͼ��������Ҫȫ�棬�����п��������ͣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ�����ڸ��˵�ϰ�߲�ͬ��˫�ֽ���ʱ���ִ�Ĵָ���ϻ����ִ�Ĵָ������һ������¼�������ʦ�����ν̵�ѧ������һ�����飬ͳ�ƽ�������ʾ��
��ͼ�����ڸ��˵�ϰ�߲�ͬ��˫�ֽ���ʱ���ִ�Ĵָ���ϻ����ִ�Ĵָ������һ������¼�������ʦ�����ν̵�ѧ������һ�����飬ͳ�ƽ�������ʾ��| 2011�� | 2012�� | 2013�� | 2014�� | 2015�� | |
| ����ʵ������� | 106 | 110 | 98 | 104 | 112 |
| ���ִ�Ĵָ���ϵ����� | 54 | 57 | 49 | 51 | 56 |
| Ƶ�� | 0.509 | 0.518 | 0.500 | 0.490 | 0.500 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3+2$\sqrt{2}$=5$\sqrt{2}$ | B�� | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{5}$ | C�� | 2$\sqrt{\frac{1}{2}}$=2 | D�� | 4$\sqrt{3}$-3$\sqrt{3}$=$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com