
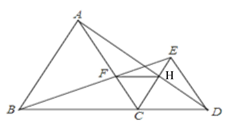
【题目】已知:点B,C,D在同一直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H,
(1)求证:△BCE≌△ACD;
(2)判断△CFH的形状并说明理由.
(3)写出FH与BD的位置关系,并说明理由.
【答案】(1)证明见解析;(2)△CFH是等边三角形,理由见解析;(3)![]() ,理由见解析.
,理由见解析.
【解析】试题分析:(1)利用等边三角形的性质得出条件,可证明:△BCE≌△ACD;
(2)利用△BCE≌△ACD得出∠CBF=∠CAH,再运用平角定义得出∠BCF=∠ACH进而得出△BCF≌△ACH因此CF=CH,再由已知条件从而可判断出△CFH的形状;
(3)由CF=CH和∠ACH=60°根据“有一个角是60°的三角形是等边三角形可得△CFH是等边三角形,从而可作出判断.
试题解析:(1)![]() △ABC和△CDE是等边三角形,
△ABC和△CDE是等边三角形, ![]() ,
, ![]() ,
,
![]() (等式的性质),
(等式的性质),
在△BEC和△ADC中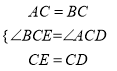 ,
,
![]() △BEC≌△ADC(SAS);
△BEC≌△ADC(SAS);
(2))△CFH是等边三角形,理由:
∵△BEC≌△ADC(已证),![]() ,
,
在△BCF和△ACH中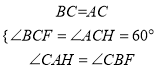 ,
,
![]() △BCF≌△ACH(ASA),,
△BCF≌△ACH(ASA),,![]() ,
,
又![]() ,
,
![]() △CFH是等边三角形;
△CFH是等边三角形;
(3)![]() ,理由:
,理由:
![]() △CFH是等边三角形,
△CFH是等边三角形,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
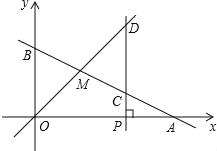
【题目】如图,已知函数y=kx+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点A的坐标为(6,0),点M的横坐标为2,过点P(a,0),作x轴的垂线,分别交函数y=kx+b和y=x的图象于点C、D.
(1)求函数y=kx+b的表达式;
(2)若点M是线段OD的中点,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( ).
A.所有的有理数都有相反数
B.正数与负数互为相反数
C.在一个数的前面添上“-”,就得到它的相反数.
D.在数轴上到原点距离相等的两个点所表示的数是互为相反数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)如图1,已知点B(0,6),点C为x轴上一动点,连接BC,△ODC和△EBC都是等边三角形.
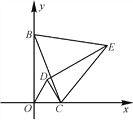
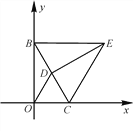
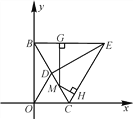
图1 图2 图3
(1)求证:DE=BO;
(2)如图2,当点D恰好落在BC上时.
①求OC的长及点E的坐标;
②在x轴上是否存在点P,使△PEC为等腰三角形?若存在,写出点P的坐标;若不存在,说明理由;
③如图3,点M是线段BC上的动点(点B,C除外),过点M作MG⊥BE于点G,MH⊥CE于点H,当点M运动时,MH+MG的值是否发生变化?若不会变化,直接写出MH+MG的值;若会变化,简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com