
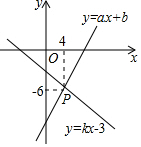 如图,已知函数y=ax+b与函数y=kx-3的图象交于点P(4,-6),则不等式ax+b≤kx-3<0的解集是-4<x≤4.
如图,已知函数y=ax+b与函数y=kx-3的图象交于点P(4,-6),则不等式ax+b≤kx-3<0的解集是-4<x≤4. 分析 先把P点坐标代入y=kx-3得k=-$\frac{3}{4}$,则可确定函数y=-$\frac{3}{4}$x-3与x轴的交点坐标,然后利用函数图象写出在x轴下方,且直线y=ax+b不在直线y=kx-3上方所对应的自变量的范围即可.
解答 解:如图,把P(4,-6)代入y=kx-3得4k-3=-6,解得k=-$\frac{3}{4}$,
则y=0时,y=-$\frac{3}{4}$x-3=0,解得x=-4,
所以不等式ax+b≤kx-3<0的解集为-4<x≤4.
故答案为-4<x≤4.
点评 本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.


科目:初中数学 来源: 题型:解答题
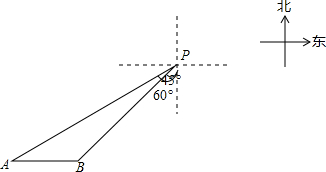 一艘轮船位于灯塔P南偏西60°方向,距离灯塔200海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)?
一艘轮船位于灯塔P南偏西60°方向,距离灯塔200海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+c与y轴交于点A(0,-$\sqrt{3}$),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
如图,抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+c与y轴交于点A(0,-$\sqrt{3}$),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x5•x5=x10 | B. | x5+x5=2x5 | ||
| C. | (-x5)5=-x25 | D. | (2x2y)3÷($\frac{1}{4}$xy3)=$\frac{1}{2}$x5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
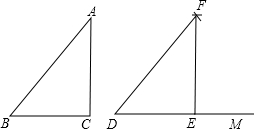 小明用如图所示的方法画出了与△ABC全等的△DEF,他的具体画法是:①画射线DM,在射线DM上截取DE=BC;②以点D为圆心,BA长为半径画弧,以点E为圆心,CA长为半径画弧,画弧相交于点F;③联结FD,FE;这样△DEF就是所要画的三角形,小明这样画图的依据是全等三角形判定方法中的( )
小明用如图所示的方法画出了与△ABC全等的△DEF,他的具体画法是:①画射线DM,在射线DM上截取DE=BC;②以点D为圆心,BA长为半径画弧,以点E为圆心,CA长为半径画弧,画弧相交于点F;③联结FD,FE;这样△DEF就是所要画的三角形,小明这样画图的依据是全等三角形判定方法中的( )| A. | 边角边 | B. | 角边角 | C. | 角角边 | D. | 边边边 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
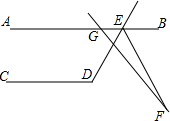 如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F的度数是( )
如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F的度数是( )| A. | 10.5° | B. | 9.5° | C. | 8.5° | D. | 8° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com