
【题目】已知等边△ABC的边长为2,点D在射线CB上,点E在射线AC上,且AD=AE,∠EDC=15°,则线段CD=_______.
【答案】1或4
【解析】
如图1和图2,分点D、点E分别在线段CB和AC上和点D、点E分别在CB的延长线和AC的延长线上两种情形画出符合题意的图形,再结合已知条件分别进行分析解答即可.
(1)如图1,当点D、点E分别在线段CB和AC上时,
∵△ABC是等边三角形,
∴∠C=∠BAC=60°,
∵∠CDE=15°,
∴∠AED=∠CDE+∠C=15°+60°=75°,
∵AD=AE,
∴∠AED=∠AED=75°,
∴∠DAE=180°-75°-75°=30°,
∴∠BAD=60°-30°=30°=∠CAD,
∴AD是等边三角形BC边上的中线,
∴CD=![]() BC=1;
BC=1;
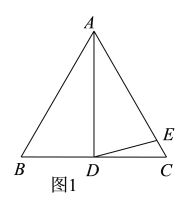
(2)如图2,当点D、点E分别在CB的延长线和AC的延长线上时,
∵△ABC是等边三角形,
∴∠ACB =60°,
∵∠CDE=15°,
∴∠E=∠ACB-∠CDE=60°-15°=45°,
∵AD=AE,
∴∠ADE=∠E=45°,
∴∠DAE=180°-45°-45°=90°,
∴∠ADC=180°-∠DAE-∠ACB=30°,
∴CD=2AC=4.
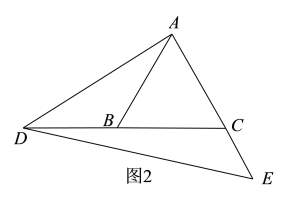
综合(1)(2)可得:CD=1或4.
故答案为:1或4.


科目:初中数学 来源: 题型:
【题目】(8分)某市团委在2015年3月初组成了300个学雷锋小组,现从中随机抽取6个小组在3月份做好事件数的统计情况如图所示:
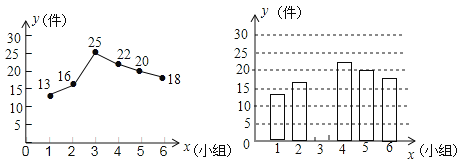
(1)这6个学雷锋小组在2015年3月份共做好事多少件?
(2)补全条形统计图;
(3)请估计该市300个学雷锋小组在2015年3月份共做好事多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732).
≈1.732).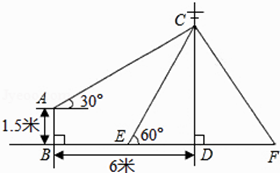
查看答案和解析>>
科目:初中数学 来源: 题型:
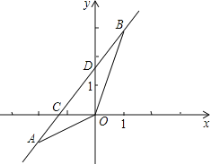
【题目】如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
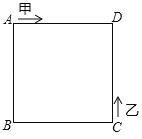
【题目】如图,甲、乙两动点分别从正方形ABCD的顶点A.C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2015次相遇在边________上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店从机械厂购进甲、乙两种零件进行销售,若甲种零件每件的进价是乙种零件每件进价的![]() ,用1600元单独购进一种零件时,购进甲种零件的数量比乙种零件的数量多4件.
,用1600元单独购进一种零件时,购进甲种零件的数量比乙种零件的数量多4件.
(1)求每件甲种零件和每件乙种零件的进价分别为多少元?
(2)若该商店计划购进甲、乙两种零件共110件,准备将零件批发给零售商. 甲种零件的批发价是每件100元,乙种零件的批发价是每件130元,该商店计划将这批产品全部售出从零售商处获利不低于3000元,那么该商店最多购进多少件甲种零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
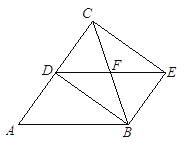
【题目】如图,在△ABC中,AB=BC,BD平分∠ABC.过点D作AB的平行线,过点B作AC的平行线,两平行线相交于点E, BC交DE于点F,连接CE.求证:四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com