
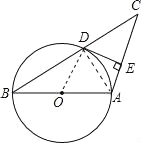
【题目】如图所示,已知AB是圆O的直径,圆O过BC的中点D,且DE⊥AC.
(1)求证:DE是圆O的切线;
(2)若∠C=30°,CD=10cm,求圆O的半径.

【答案】
【解析】
试题分析:(1)连接OD,利用三角形的中位线定理可得出OD∥AC,再利用平行线的性质就可证明DE是圆O的切线.
(2)利用30°特殊角度,可求出AD的长,由两直线平行同位角相等,可得出∠ODB=∠C=30°,从而△ABD为直角三角形,圆O的半径可求.
试题解析:(1)连接OD,∵D是BC的中点,O为AB的中点,∴OD∥AC.
又∵DE⊥AC,∴OD⊥DE,∵OD为半径,∴DE是圆O的切线.
(2)连接AD;∵AB是圆O的直径,∴∠ADB=90°=∠ADC,
∴△ADC是直角三角形.∵∠C=30°,CD=10,∴AD=![]() .
.
∵OD∥AC,OD=OB,∴∠B=30°,∴△OAD是等边三角形,∴OD=AD=![]() ,
,
∴圆O的半径为![]() cm.
cm.


科目:初中数学 来源: 题型:
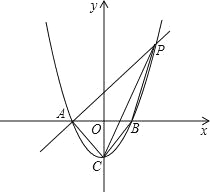
【题目】已知如图:抛物线y=x2﹣1与x轴交于A、B两点,与y轴交于点C.
(1)求A、B、C三点的坐标.
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现定义两种运算“⊕”“*”.对于任意两个整数,a⊕b=a+b-1,a*b=a×b-1,则6⊕[8*(x⊕3)]=52,则x的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com