
【题目】已知:AB为⊙O的直径,点C,D在⊙O上,![]() 连接AD,OC.
连接AD,OC.
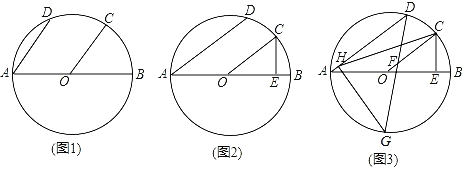
(1)如图1,求证:AD∥OC;
(2)如图2,过点C作CE⊥AB于点E,求证:AD=2OE;
(3)如图3,在(2)的条件下,点F在OC上,且OF=BE,连接DF并延长交⊙O于点G,过点G作CH⊥AD于点H,连接CH,若∠CFG=135°,CE=3,求CH的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)如图1(见解析),先根据圆心角定理得出![]() ,从而可得
,从而可得![]() ,再根据圆周角定理可得
,再根据圆周角定理可得![]() ,从而可得
,从而可得![]() ,然后根据平行线的判定即可得证;
,然后根据平行线的判定即可得证;
(2)如图2(见解析),先根据圆周角定理得出![]() ,再根据题(1)的结论、直角三角形的性质得出
,再根据题(1)的结论、直角三角形的性质得出![]() ,然后根据圆周角定理、圆心角定理可得
,然后根据圆周角定理、圆心角定理可得![]() ,最后根据垂径定理、中位线定理得出
,最后根据垂径定理、中位线定理得出![]() ,由此即可得证;
,由此即可得证;
(3)如图3(见解析),先根据圆周角定理、平行线的性质得出![]() ,再根据垂径定理可得
,再根据垂径定理可得![]() ,然后根据三角形全等的判定定理与性质得出
,然后根据三角形全等的判定定理与性质得出![]() ,从而可得
,从而可得![]() ,在
,在![]() 中,利用勾股定理可得
中,利用勾股定理可得![]() ,又根据直角三角形的性质、矩形的性质、圆的相交弦定理得出
,又根据直角三角形的性质、矩形的性质、圆的相交弦定理得出![]() ,
,![]() ,从而可得
,从而可得![]() ,最后利用勾股定理即可得.
,最后利用勾股定理即可得.
(1)如图1,连接OD
∵![]()
∴![]()
![]()
![]()
由圆周角定理得:![]()
∴![]()
∴![]() ;
;

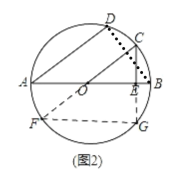
(2)如图2,延长CO交圆O于F,延长CE交圆O于G,连接FG,BD
则![]()
∵![]() 于E
于E
∴![]() ,
,![]()
∴![]()
∵![]() ,
,![]()
∴![]()
![]()
∴![]()
∵![]() ,
,![]()
![]() OE是
OE是![]() 的中位线
的中位线
∴![]()
∴![]() ,即
,即![]() ;
;
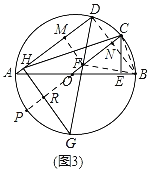
(3)如图3,延长CO交圆O于P,连接BD交OC于N,作PM⊥AD于M,连接BC、BF,则![]()
∵![]()
∴![]()
∴![]()
∵![]() 于E
于E
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]() ,
,![]()
设![]() ,则
,则![]()
在![]() 中,
中,![]() ,即
,即![]() ,解得
,解得![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
设CP交HG于R
∵![]()
∴![]()
∴![]()
∴![]() ,
,![]() ,
,![]()
又∵![]() ,即
,即![]()
解得![]()
∴![]()
在![]() 中,
中,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,BC是⊙O的直径,A是弦BD延长线上一点,切线DE平分AC于E.

(1)求证:AC是⊙O的切线;
(2)若AD∶DB=3∶2,AC=15,求⊙O的直径;
(3)在(2)的条件下,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
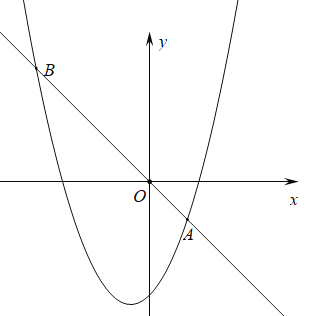
【题目】已知抛物线![]() 经过点
经过点![]() ,
,![]() .把抛物线
.把抛物线![]() 与线段
与线段![]() 围成的封闭图形记作
围成的封闭图形记作![]() .
.
(1)求此抛物线的解析式;
(2)点![]() 为图形
为图形![]() 中的抛物线上一点,且点
中的抛物线上一点,且点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 作
作![]() 轴,交线段
轴,交线段![]() 于点
于点![]() .当
.当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求![]() 的值;
的值;
(3)点![]() 是直线
是直线![]() 上一点,且点
上一点,且点![]() 的横坐标为
的横坐标为![]() ,以线段
,以线段![]() 为边作正方形
为边作正方形![]() ,且使正方形
,且使正方形![]() 与图形
与图形![]() 在直线
在直线![]() 的同侧,当
的同侧,当![]() ,
,![]() 两点中只有一个点在图形
两点中只有一个点在图形![]() 的内部时,请直接写出
的内部时,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实践小组想利用镜子的反射测量池塘边一棵树的高度AB.测量和计算的部分步骤如下:

①如图,树与地面垂直,在地面上的点C处放置一块镜子,小明站在BC的延长线上,当小明在镜子中刚好看到树的顶点A时,测得小明到镜子的距离CD=2米,小明的眼睛E到地面的距离ED=1.5米;
②将镜子从点C沿BC的延长线向后移动10米到点F处,小明向后移动到点H处时,小明的眼睛G又刚好在镜子中看到树的顶点A,这时测得小明到镜子的距离FH=3米;
③计算树的高度AB;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 的直径
的直径![]() ,
,![]() 、
、![]() 为圆周上两点,且
为圆周上两点,且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
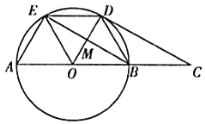
(1)求证:![]() 为
为![]() 切线;
切线;
(2)填空:①当四边形![]() 为菱形,则
为菱形,则![]() 的度数为________;
的度数为________;
②当![]() 时,四边形
时,四边形![]() 的面积为________.
的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
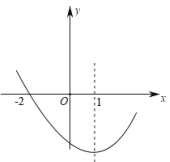
【题目】如图,二次函数![]() 的图象过点
的图象过点![]() ,对称轴为直
,对称轴为直![]() 线,下列结论中一定正确的是____________(填序号即可).
线,下列结论中一定正确的是____________(填序号即可).
①![]() ;
;
②若![]() 是抛物线上的两点,当
是抛物线上的两点,当![]() 时,
时,![]()
③若方程![]() 的两根为
的两根为![]() ,且
,且![]() ,则
,则![]()
④![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() . 点
. 点![]() 是平面内不与点
是平面内不与点![]() 重合的任意一点, 连接
重合的任意一点, 连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]()
(1)动手操作
如图1,当![]() 时,我们通过用 刻度尺和量角器度量发现:
时,我们通过用 刻度尺和量角器度量发现:
![]() 的值是
的值是![]() ;直线
;直线![]() 与直线
与直线![]() 相交所成的较小角的度数是
相交所成的较小角的度数是![]() ;
;
请证明以上结论正确.
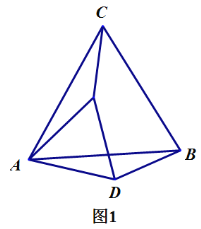
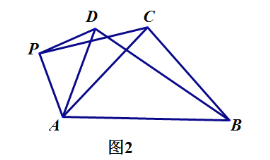
(2)类比探究
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的较小角的度数,并就图2的情形说明理由.
相交所成的较小角的度数,并就图2的情形说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com