
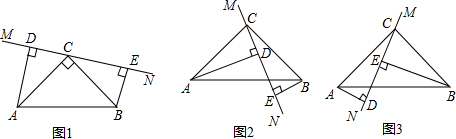
 如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于( )
如图,⊙O的半径为20,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=12.延长BC,与⊙O分别交于D,E两点,则CE-BD的值等于( )| A. | $\frac{24}{5}$ | B. | $\frac{28}{5}$ | C. | $\frac{36}{5}$ | D. | $\frac{48}{5}$ |
分析 连接OE,作ON⊥DE,由垂径定理得EN=DN,在Rt△AOB中利用勾股定理求出OB的长,利用三角形的面积公式求出ON的长,在Rt△OCN中,利用勾股定理求出CN的长,进而可得出BN的长,由CE-BD=(EN-CN)-(DN-BN)=BN-CN即可得出结论.
解答 解:如图,连接OE,作ON⊥DE,
∴EN=DN,
∵在Rt△AOB中,OA=20,AB=OC=12,
∴OB=$\sqrt{{OA}^{2}{-AB}^{2}}$=$\sqrt{{20}^{2}{-12}^{2}}$=16,
∴ON=$\frac{OB•OC}{BC}$=$\frac{16×12}{20}$=$\frac{48}{5}$,
在Rt△OCN中,
CN=$\sqrt{{OC}^{2}{-ON}^{2}}$=$\frac{36}{5}$,
∵BN=BC-CN=20-$\frac{36}{5}$=$\frac{64}{5}$,
∴CE-BD=(EN-CN)-(DN-BN)=BN-CN=$\frac{64}{5}$-$\frac{36}{5}$=$\frac{28}{5}$,
故选B.
点评 本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理进行解答是解答此题的关键.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成如表如下:
某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成如表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | m | 0.45 |
| 80≤x<90 | 60 | n |
| 90≤x<100 | 20 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象经过点(2,2) | B. | y随x的增大而减小 | ||
| C. | 图象位于第一、三象限 | D. | 当x<1时,y的值都大于2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
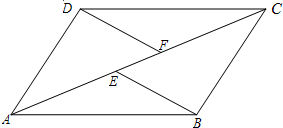 如图,E、F是四边形ABCD的对角线AC上两点,AE=CF,DF∥BE,DF=BE.
如图,E、F是四边形ABCD的对角线AC上两点,AE=CF,DF∥BE,DF=BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com